Info

新版网站会员 限时优惠；算法可视化编辑器上线，点击体验！

读完本文，你不仅学会了算法套路，还可以顺便解决如下题目：

LeetCode	力扣	难度
1514. Path with Maximum Probability	1514. 概率最大的路径	🟠
1631. Path With Minimum Effort	1631. 最小体力消耗路径	🟠
743. Network Delay Time	743. 网络延迟时间	🟠

其实，很多算法的底层原理异常简单，无非就是一步一步延伸，变得看起来好像特别复杂，特别牛逼。

但如果你看过历史文章，应该可以对算法形成自己的理解，就会发现很多算法都是换汤不换药，毫无新意，非常枯燥。

比如，东哥手把手带你刷二叉树（总纲） 中说二叉树非常重要，你把这个结构掌握了，就会发现 动态规划，分治算法，回溯（DFS）算法，BFS 算法框架，Union-Find 并查集算法，二叉堆实现优先级队列 就是把二叉树翻来覆去的运用。

那么本文又要告诉你，Dijkstra 算法（一般音译成迪杰斯特拉算法）无非就是一个 BFS 算法的加强版，它们都是从二叉树的层序遍历衍生出来的。

这也是为什么我在 学习数据结构和算法的框架思维 中这么强调二叉树的原因。

下面我们由浅入深，从二叉树的层序遍历聊到 Dijkstra 算法，给出 Dijkstra 算法的代码框架，顺手秒杀几道运用 Dijkstra 算法的题目。

图的抽象

前文 图论第一期：遍历基础 说过「图」这种数据结构的基本实现，图中的节点一般就抽象成一个数字（索引），图的具体实现一般是「邻接矩阵」或者「邻接表」。

比如上图这幅图用邻接表和邻接矩阵的存储方式如下：

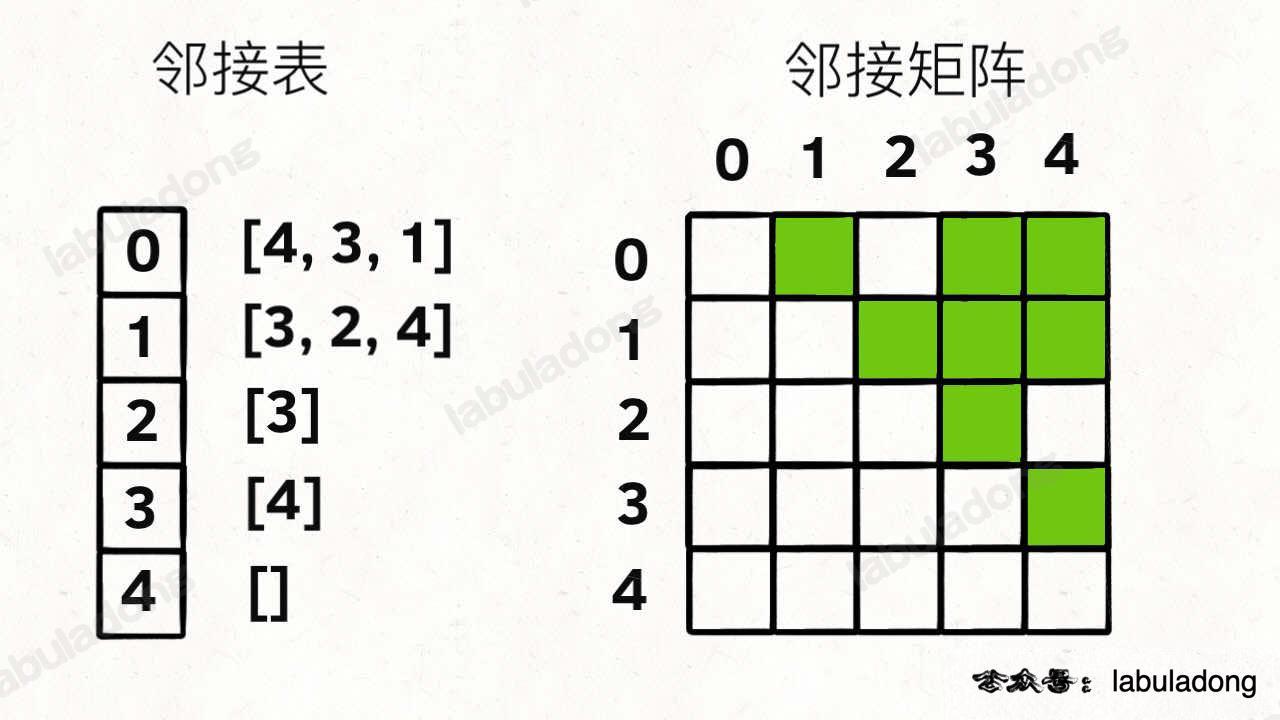
前文 图论第二期：拓扑排序 告诉你，我们用邻接表的场景更多，结合上图，一幅图可以用如下 Java 代码表示：

java 🟢

// graph[s] 存储节点 s 指向的节点（出度）
List<Integer>[] graph;

cpp 🤖

// 注意：cpp 代码由 chatGPT🤖 根据我的 java 代码翻译，旨在帮助不同背景的读者理解算法逻辑。
// 本代码不保证正确性，仅供参考。如有疑惑，可以参照我写的 java 代码对比查看。

// vector<type> name 表示定义一个元素类型为 type 的动态数组 name
vector<int>[] graph; // graph[s] 存储节点 s 指向的节点（出度）

python 🤖

# 注意：python 代码由 chatGPT🤖 根据我的 java 代码翻译，旨在帮助不同背景的读者理解算法逻辑。
# 本代码不保证正确性，仅供参考。如有疑惑，可以参照我写的 java 代码对比查看。

# graph[s] 存储节点 s 指向的节点（出度）
graph: List[List[int]] = []

go 🤖

// 注意：go 代码由 chatGPT🤖 根据我的 java 代码翻译，旨在帮助不同背景的读者理解算法逻辑。
// 本代码不保证正确性，仅供参考。如有疑惑，可以参照我写的 java 代码对比查看。

// graph[s] 存储节点 s 指向的节点（出度）
var graph [][]int

javascript 🤖

// 注意：javascript 代码由 chatGPT🤖 根据我的 java 代码翻译，旨在帮助不同背景的读者理解算法逻辑。
// 本代码不保证正确性，仅供参考。如有疑惑，可以参照我写的 java 代码对比查看。

// graph[s] 存储节点 s 指向的节点（出度）
var graph;

如果你想把一个问题抽象成「图」的问题，那么首先要实现一个 API adj：

java 🟢

// 输入节点 s 返回 s 的相邻节点
List<Integer> adj(int s);

cpp 🤖

// 注意：cpp 代码由 chatGPT🤖 根据我的 java 代码翻译，旨在帮助不同背景的读者理解算法逻辑。
// 本代码不保证正确性，仅供参考。如有疑惑，可以参照我写的 java 代码对比查看。

// 输入节点 s 返回 s 的相邻节点
vector<int> adj(int s);

python 🤖

# 注意：python 代码由 chatGPT🤖 根据我的 java 代码翻译，旨在帮助不同背景的读者理解算法逻辑。
# 本代码不保证正确性，仅供参考。如有疑惑，可以参照我写的 java 代码对比查看。

# 输入节点 s 返回 s 的相邻节点
def adj(s: int) -> List[int]:

go 🤖

// 注意：go 代码由 chatGPT🤖 根据我的 java 代码翻译，旨在帮助不同背景的读者理解算法逻辑。
// 本代码不保证正确性，仅供参考。如有疑惑，可以参照我写的 java 代码对比查看。

// 输入节点 s 返回 s 的相邻节点
func adj(s int) []int {
}

javascript 🤖

// 注意：javascript 代码由 chatGPT🤖 根据我的 java 代码翻译，旨在帮助不同背景的读者理解算法逻辑。
// 本代码不保证正确性，仅供参考。如有疑惑，可以参照我写的 java 代码对比查看。

// 输入节点 s 返回 s 的相邻节点
var adj = function(s) {
    var adjList = [];
    // implementation
    return adjList;
};

类似多叉树节点中的 children 字段记录当前节点的所有子节点，adj(s) 就是计算一个节点 s 的相邻节点。

比如上面说的用邻接表表示「图」的方式，adj 函数就可以这样表示：

java 🟢

List<Integer>[] graph;

// 输入节点 s，返回 s 的相邻节点
List<Integer> adj(int s) {
    return graph[s];
}

cpp 🤖

// 注意：cpp 代码由 chatGPT🤖 根据我的 java 代码翻译，旨在帮助不同背景的读者理解算法逻辑。
// 本代码不保证正确性，仅供参考。如有疑惑，可以参照我写的 java 代码对比查看。

vector<int>* graph;

// 输入节点 s，返回 s 的相邻节点
vector<int> adj(int s) {
    return graph[s];
}

python 🤖

# 注意：python 代码由 chatGPT🤖 根据我的 java 代码翻译，旨在帮助不同背景的读者理解算法逻辑。
# 本代码不保证正确性，仅供参考。如有疑惑，可以参照我写的 java 代码对比查看。

from typing import List

graph: List[List[int]] = []

# 输入节点 s，返回 s 的相邻节点
def adj(s: int) -> List[int]:
    return graph[s]

go 🤖

// 注意：go 代码由 chatGPT🤖 根据我的 java 代码翻译，旨在帮助不同背景的读者理解算法逻辑。
// 本代码不保证正确性，仅供参考。如有疑惑，可以参照我写的 java 代码对比查看。

var graph []List[int]

// 输入节点 s，返回 s 的相邻节点
func adj(s int) []int {
    return graph[s]
}

javascript 🤖

// 注意：javascript 代码由 chatGPT🤖 根据我的 java 代码翻译，旨在帮助不同背景的读者理解算法逻辑。
// 本代码不保证正确性，仅供参考。如有疑惑，可以参照我写的 java 代码对比查看。

var graph;

// 输入节点 s，返回 s 的相邻节点
function adj(s) {
    return graph[s];
}

当然，对于「加权图」，我们需要知道两个节点之间的边权重是多少，所以还可以抽象出一个 weight 方法：

java 🟢

// 返回节点 from 到节点 to 之间的边的权重
int weight(int from, int to);

cpp 🤖

// 注意：cpp 代码由 chatGPT🤖 根据我的 java 代码翻译，旨在帮助不同背景的读者理解算法逻辑。
// 本代码不保证正确性，仅供参考。如有疑惑，可以参照我写的 java 代码对比查看。

// 返回节点 from 到节点 to 之间的边的权重
int weight(int from, int to);

python 🤖

# 注意：python 代码由 chatGPT🤖 根据我的 java 代码翻译，旨在帮助不同背景的读者理解算法逻辑。
# 本代码不保证正确性，仅供参考。如有疑惑，可以参照我写的 java 代码对比查看。

# 返回节点 from 到节点 to 之间的边的权重
def weight(from_node: int, to_node: int) -> int:

go 🤖

// 注意：go 代码由 chatGPT🤖 根据我的 java 代码翻译，旨在帮助不同背景的读者理解算法逻辑。
// 本代码不保证正确性，仅供参考。如有疑惑，可以参照我写的 java 代码对比查看。

// weight 返回节点 from 到节点 to 之间的边的权重
func weight(from, to int) int {}

javascript 🤖

// 注意：javascript 代码由 chatGPT🤖 根据我的 java 代码翻译，旨在帮助不同背景的读者理解算法逻辑。
// 本代码不保证正确性，仅供参考。如有疑惑，可以参照我写的 java 代码对比查看。

var weight = function (from, to) {
  // 返回节点 from 到节点 to 之间的边的权重
};

这个 weight 方法可以根据实际情况而定，因为不同的算法题，题目给的「权重」含义可能不一样，我们存储权重的方式也不一样。

有了上述基础知识，就可以搞定 Dijkstra 算法了，下面我给你从二叉树的层序遍历开始推演出 Dijkstra 算法的实现。

二叉树层级遍历和 BFS 算法

我们之前说过二叉树的层级遍历框架：

java 🟢

// 输入一棵二叉树的根节点，层序遍历这棵二叉树
void levelTraverse(TreeNode root) {
    if (root == null) return 0;
    Queue<TreeNode> q = new LinkedList<>();
    q.offer(root);

    int depth = 1;
    // 从上到下遍历二叉树的每一层
    while (!q.isEmpty()) {
        int sz = q.size();
        // 从左到右遍历每一层的每个节点
        for (int i = 0; i < sz; i++) {
            TreeNode cur = q.poll();
            printf("节点 %s 在第 %s 层", cur, depth);

            // 将下一层节点放入队列
            if (cur.left != null) {
                q.offer(cur.left);
            }
            if (cur.right != null) {
                q.offer(cur.right);
            }
        }
        depth++;
    }
}

cpp 🤖

// 注意：cpp 代码由 chatGPT🤖 根据我的 java 代码翻译，旨在帮助不同背景的读者理解算法逻辑。
// 本代码不保证正确性，仅供参考。如有疑惑，可以参照我写的 java 代码对比查看。

// 输入一棵二叉树的根节点，层序遍历这棵二叉树
int levelTraverse(TreeNode* root) {
    if (root == nullptr) return 0;
    queue<TreeNode*> q;
    q.push(root);

    int depth = 1;
    // 从上到下遍历二叉树的每一层
    while (!q.empty()) {
        int sz = q.size();
        // 从左到右遍历每一层的每个节点
        for (int i = 0; i < sz; i++) {
            TreeNode* cur = q.front();
            q.pop();
            printf("节点 %s 在第 %s 层", cur, depth);

            // 将下一层节点放入队列
            if (cur->left != nullptr) {
                q.push(cur->left);
            }
            if (cur->right != nullptr) {
                q.push(cur->right);
            }
        }
        depth++;
    }
    return depth;
}

python 🤖

# 注意：python 代码由 chatGPT🤖 根据我的 java 代码翻译，旨在帮助不同背景的读者理解算法逻辑。
# 本代码不保证正确性，仅供参考。如有疑惑，可以参照我写的 java 代码对比查看。

# 输入一棵二叉树的根节点，层序遍历这棵二叉树
def levelTraverse(root: TreeNode):
    if root == None:
        return 0
    q = []
    q.append(root)

    depth = 1
    # 从上到下遍历二叉树的每一层
    while len(q) > 0:
        sz = len(q)
        # 从左到右遍历每一层的每个节点
        for i in range(sz):
            cur = q.pop(0)
            printf("节点 %s 在第 %s 层", cur, depth)

            # 将下一层节点放入队列
            if cur.left != None:
                q.append(cur.left)
            if cur.right != None:
                q.append(cur.right)
        depth += 1

go 🤖

// 注意：go 代码由 chatGPT🤖 根据我的 java 代码翻译，旨在帮助不同背景的读者理解算法逻辑。
// 本代码不保证正确性，仅供参考。如有疑惑，可以参照我写的 java 代码对比查看。

// 输入一棵二叉树的根节点，层序遍历这棵二叉树
func levelTraverse(root *TreeNode) {
    if root == nil {
        return 0
    }
    q := make([]*TreeNode, 0)
    q = append(q, root)

    depth := 1
    // 从上到下遍历二叉树的每一层
    for len(q) != 0 {
        sz := len(q)
        // 从左到右遍历每一层的每个节点
        for i := 0; i < sz; i++ {
            cur := q[i]
            fmt.Printf("节点 %v 在第 %v 层\n", cur, depth)

            // 将下一层节点放入队列
            if cur.left != nil {
                q = append(q, cur.left)
            }
            if cur.right != nil {
                q = append(q, cur.right)
            }
        }
        q = q[sz:]
        depth++
    }
}

javascript 🤖

// 注意：javascript 代码由 chatGPT🤖 根据我的 java 代码翻译，旨在帮助不同背景的读者理解算法逻辑。
// 本代码不保证正确性，仅供参考。如有疑惑，可以参照我写的 java 代码对比查看。

var levelTraverse = function(root) {
    if (!root) return 0;
    let q = [];
    q.push(root);

    let depth = 1;
    // 从上到下遍历二叉树的每一层
    while (q.length !== 0) {
        let sz = q.length;
        // 从左到右遍历每一层的每个节点
        for (let i = 0; i < sz; i++) {
            let cur = q.shift();
            console.log(`节点 ${cur} 在第 ${depth} 层`);

            // 将下一层节点放入队列
            if (cur.left !== null) {
                q.push(cur.left);
            }
            if (cur.right !== null) {
                q.push(cur.right);
            }
        }
        depth++;
    }
};

我们先来思考一个问题，注意二叉树的层级遍历 while 循环里面还套了个 for 循环，为什么要这样？

while 循环和 for 循环的配合正是这个遍历框架设计的巧妙之处：

while 循环控制一层一层往下走，for 循环利用 sz 变量控制从左到右遍历每一层二叉树节点。

注意我们代码框架中的 depth 变量，其实就记录了当前遍历到的层数。换句话说，每当我们遍历到一个节点 cur，都知道这个节点属于第几层。

算法题经常会问二叉树的最大深度呀，最小深度呀，层序遍历结果呀，等等问题，所以记录下来这个深度 depth 是有必要的。

基于二叉树的遍历框架，我们又可以扩展出多叉树的层序遍历框架：

java 🟢

// 输入一棵多叉树的根节点，层序遍历这棵多叉树
void levelTraverse(TreeNode root) {
    if (root == null) return;
    Queue<TreeNode> q = new LinkedList<>();
    q.offer(root);

    int depth = 1;
    // 从上到下遍历多叉树的每一层
    while (!q.isEmpty()) {
        int sz = q.size();
        // 从左到右遍历每一层的每个节点
        for (int i = 0; i < sz; i++) {
            TreeNode cur = q.poll();
            printf("节点 %s 在第 %s 层", cur, depth);

            // 将下一层节点放入队列
            for (TreeNode child : cur.children) {
                q.offer(child);
            }
        }
        depth++;
    }
}

cpp 🤖

// 注意：cpp 代码由 chatGPT🤖 根据我的 java 代码翻译，旨在帮助不同背景的读者理解算法逻辑。
// 本代码不保证正确性，仅供参考。如有疑惑，可以参照我写的 java 代码对比查看。

void levelTraverse(TreeNode* root) {
    if (root == nullptr) return;
    queue<TreeNode*> q;
    q.push(root);

    int depth = 1;
    while (!q.empty()) {
        int sz = q.size();
        for (int i = 0; i < sz; i++) {
            TreeNode* cur = q.front();
            q.pop();
            printf("节点 %s 在第 %s 层", cur, depth);

            for (auto child : cur->children) {
                q.push(child);
            }
        }
        depth++;
    }
}

python 🤖

# 注意：python 代码由 chatGPT🤖 根据我的 java 代码翻译，旨在帮助不同背景的读者理解算法逻辑。
# 本代码不保证正确性，仅供参考。如有疑惑，可以参照我写的 java 代码对比查看。

from typing import Optional
from collections import deque

class TreeNode:
    def __init__(self, val: Optional[int] = None, children: Optional[List['TreeNode']] = None):
        self.val = val
        self.children = children or []

# 输入一棵多叉树的根节点，层序遍历这棵多叉树
def levelTraverse(root: TreeNode) -> None:
    if not root:
        return
        
    q = deque([root])
    depth = 1
    # 从上到下遍历多叉树的每一层
    while q:
        sz = len(q)
        # 从左到右遍历每一层的每个节点
        for i in range(sz):
            cur = q.popleft()
            print("节点 {} 在第 {} 层".format(cur.val, depth))

            # 将下一层节点放入队列
            for child in cur.children:
                q.append(child)
        depth += 1

go 🤖

// 注意：go 代码由 chatGPT🤖 根据我的 java 代码翻译，旨在帮助不同背景的读者理解算法逻辑。
// 本代码不保证正确性，仅供参考。如有疑惑，可以参照我写的 java 代码对比查看。

// 输入一棵多叉树的根节点，层序遍历这棵多叉树
func levelTraverse(root *TreeNode) {
    if root == nil {
        return
    }
    q := make([]*TreeNode, 0)
    q = append(q, root)
    depth := 1

    // 从上到下遍历多叉树的每一层
    for len(q) > 0 {
        sz := len(q)
        // 从左到右遍历每一层的每个节点
        for i := 0; i < sz; i++ {
            cur := q[i]
            fmt.Printf("节点 %s 在第 %d 层", cur, depth)

            // 将下一层节点放入队列
            for _, child := range cur.children {
                q = append(q, child)
            }
        }
        depth++
        q = q[sz:]
    }
}

javascript 🤖

// 注意：javascript 代码由 chatGPT🤖 根据我的 java 代码翻译，旨在帮助不同背景的读者理解算法逻辑。
// 本代码不保证正确性，仅供参考。如有疑惑，可以参照我写的 java 代码对比查看。

var levelTraverse = function(root) {
    if (root == null) return;
    var q = [];
    q.push(root);

    var depth = 1;
    while (q.length > 0) {
        var sz = q.length;
        for (var i = 0; i < sz; i++) {
            var cur = q.shift();
            console.log("节点 " + cur + " 在第 " + depth + " 层");

            for (var j = 0; j < cur.children.length; j++) {
                q.push(cur.children[j]);
            }
        }
        depth++;
    }
};

基于多叉树的遍历框架，我们又可以扩展出 BFS（广度优先搜索）的算法框架：

java 🟢

// 输入起点，进行 BFS 搜索
int BFS(Node start) {
    Queue<Node> q; // 核心数据结构
    Set<Node> visited; // 避免走回头路
    
    q.offer(start); // 将起点加入队列
    visited.add(start);

    int step = 0; // 记录搜索的步数
    while (q not empty) {
        int sz = q.size();
        /* 将当前队列中的所有节点向四周扩散一步 */
        for (int i = 0; i < sz; i++) {
            Node cur = q.poll();
            printf("从 %s 到 %s 的最短距离是 %s", start, cur, step);

            /* 将 cur 的相邻节点加入队列 */
            for (Node x : cur.adj()) {
                if (x not in visited) {
                    q.offer(x);
                    visited.add(x);
                }
            }
        }
        step++;
    }
}

cpp 🤖

// 注意：cpp 代码由 chatGPT🤖 根据我的 java 代码翻译，旨在帮助不同背景的读者理解算法逻辑。
// 本代码不保证正确性，仅供参考。如有疑惑，可以参照我写的 java 代码对比查看。

#include <queue>
#include <set>

// 输入起点，进行 BFS 搜索
int BFS(Node* start) {
    std::queue<Node*> q; // 核心数据结构
    std::set<Node*> visited; // 避免走回头路
    
    q.push(start); // 将起点加入队列
    visited.insert(start);

    int step = 0; // 记录搜索的步数
    while (!q.empty()) {
        int sz = q.size();
        /* 将当前队列中的所有节点向四周扩散一步 */
        for (int i = 0; i < sz; i++) {
            Node* cur = q.front();
            q.pop();
            printf("从 %s 到 %s 的最短距离是 %s", start->val, cur->val, step);

            /* 将 cur 的相邻节点加入队列 */
            for (Node* x : cur->adj()) {
                if (visited.count(x) == 0) {
                    q.push(x);
                    visited.insert(x);
                }
            }
        }
        step++;
    }
}

python 🤖

# 注意：python 代码由 chatGPT🤖 根据我的 java 代码翻译，旨在帮助不同背景的读者理解算法逻辑。
# 本代码不保证正确性，仅供参考。如有疑惑，可以参照我写的 java 代码对比查看。

# 输入起点，进行 BFS 搜索
def BFS(start: Node) -> int:
    # 核心数据结构
    q = [] 
    # 避免走回头路
    visited = set() 
    
    # 将起点加入队列
    q.append(start)
    visited.add(start)

    # 记录搜索的步数
    step = 0 
    while len(q) != 0:
        sz = len(q)
        # 将当前队列中的所有节点向四周扩散一步
        for i in range(sz):
            cur = q.pop(0)
            print(f"从 {start} 到 {cur} 的最短距离是 {step}")

            # 将 cur 的相邻节点加入队列
            for x in cur.adj():
                if x not in visited:
                    q.append(x)
                    visited.add(x)
        step += 1

go 🤖

// 注意：go 代码由 chatGPT🤖 根据我的 java 代码翻译，旨在帮助不同背景的读者理解算法逻辑。
// 本代码不保证正确性，仅供参考。如有疑惑，可以参照我写的 java 代码对比查看。

func BFS(start Node) int {
    q := make([]Node, 0) // 核心数据结构
    visited := make(map[Node]bool) // 避免走回头路

    q = append(q, start) // 将起点加入队列
    visited[start] = true

    step := 0 // 记录搜索的步数
    for len(q) != 0 {
        sz := len(q)
        /* 将当前队列中的所有节点向四周扩散一步 */
        for i := 0; i < sz; i++ {
            cur := q[0]
            q = q[1:]
            fmt.Printf("从 %s 到 %s 的最短距离是 %d", start, cur, step)

            /* 将 cur 的相邻节点加入队列 */
            adj := cur.adj()
            for _, x := range adj {
                if _, ok := visited[x]; !ok {
                    q = append(q, x)
                    visited[x] = true
                }
            }
        }
        step++
    }
    
    return step
}

javascript 🤖

// 注意：javascript 代码由 chatGPT🤖 根据我的 java 代码翻译，旨在帮助不同背景的读者理解算法逻辑。
// 本代码不保证正确性，仅供参考。如有疑惑，可以参照我写的 java 代码对比查看。

var BFS = function(start) {
    var q = []; // 核心数据结构
    var visited = new Set(); // 避免走回头路
    
    q.push(start); // 将起点加入队列
    visited.add(start);

    var step = 0; // 记录搜索的步数
    while (q.length !== 0) {
        var sz = q.length;
        /* 将当前队列中的所有节点向四周扩散一步 */
        for (var i = 0; i < sz; i++) {
            var cur = q.shift();
            console.log("从 " + start + " 到 " + cur + " 的最短距离是 " + step);

            /* 将 cur 的相邻节点加入队列 */
            for (var j = 0; j < cur.adj().length; j++) {
                var x = cur.adj()[j];
                if (!visited.has(x)) {
                    q.push(x);
                    visited.add(x);
                }
            }
        }
        step++;
    }
};

如果对 BFS 算法不熟悉，可以看前文 BFS 算法框架，这里只是为了让你做个对比，所谓 BFS 算法，就是把算法问题抽象成一幅「无权图」，然后继续玩二叉树层级遍历那一套罢了。

注意，我们的 BFS 算法框架也是 while 循环嵌套 for 循环的形式，也用了一个 step 变量记录 for 循环执行的次数，无非就是多用了一个 visited 集合记录走过的节点，防止走回头路罢了。

为什么这样呢？

所谓「无权图」，与其说每条「边」没有权重，不如说每条「边」的权重都是 1，从起点 start 到任意一个节点之间的路径权重就是它们之间「边」的条数，那可不就是 step 变量记录的值么？

再加上 BFS 算法利用 for 循环一层一层向外扩散的逻辑和 visited 集合防止走回头路的逻辑，当你每次从队列中拿出节点 cur 的时候，从 start 到 cur 的最短权重就是 step 记录的步数。

但是，到了「加权图」的场景，事情就没有这么简单了，因为你不能默认每条边的「权重」都是 1 了，这个权重可以是任意正数（Dijkstra 算法要求不能存在负权重边），比如下图的例子：

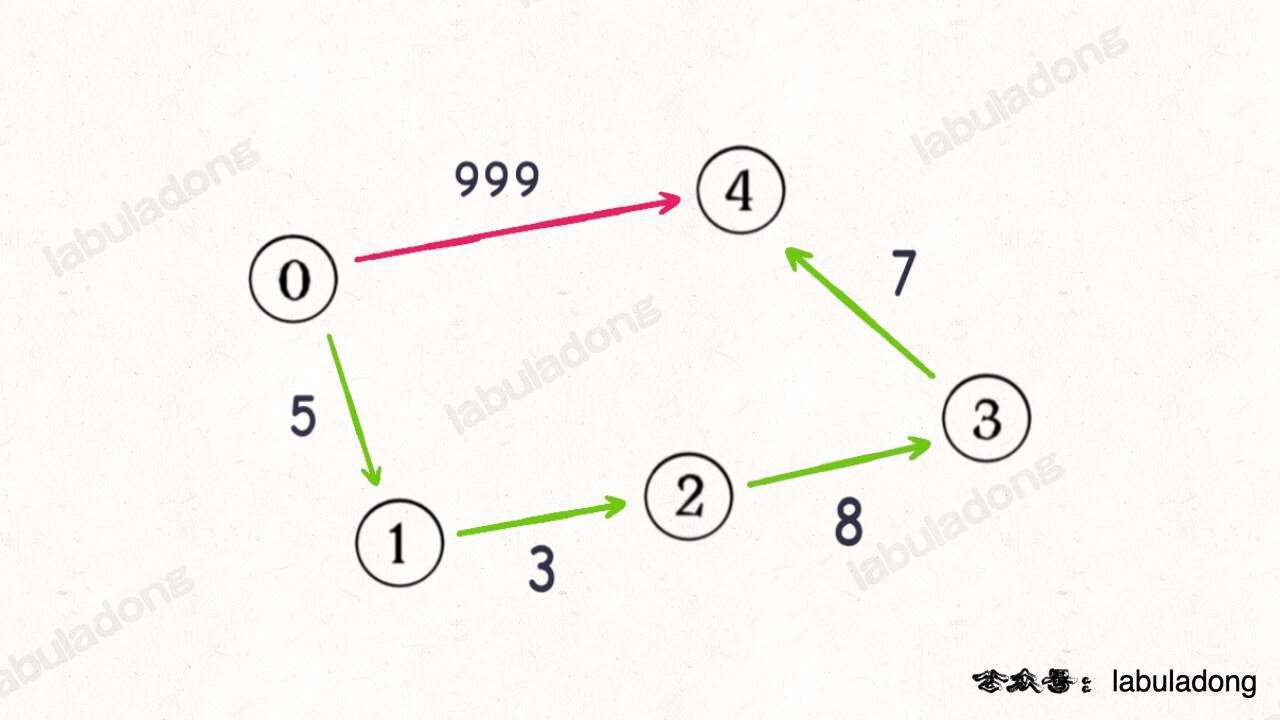
如果沿用 BFS 算法中的 step 变量记录「步数」，显然红色路径一步就可以走到终点，但是这一步的权重很大；正确的最小权重路径应该是绿色的路径，虽然需要走很多步，但是路径权重依然很小。

其实 Dijkstra 和 BFS 算法差不多，不过在讲解 Dijkstra 算法框架之前，我们首先需要对之前的框架进行如下改造：

想办法去掉 while 循环里面的 for 循环。

为什么？有了刚才的铺垫，这个不难理解，刚才说 for 循环是干什么用的来着？

是为了让二叉树一层一层往下遍历，让 BFS 算法一步一步向外扩散，因为这个层数 depth，或者这个步数 step，在之前的场景中有用。

但现在我们想解决「加权图」中的最短路径问题，「步数」已经没有参考意义了，「路径的权重之和」才有意义，所以这个 for 循环可以被去掉。

怎么去掉？就拿二叉树的层级遍历来说，其实你可以直接去掉 for 循环相关的代码：

java 🟢

// 输入一棵二叉树的根节点，遍历这棵二叉树所有节点
void levelTraverse(TreeNode root) {
    if (root == null) return 0;
    Queue<TreeNode> q = new LinkedList<>();
    q.offer(root);

    // 遍历二叉树的每一个节点
    while (!q.isEmpty()) {
        TreeNode cur = q.poll();
        printf("我不知道节点 %s 在第几层", cur);

        // 将子节点放入队列
        if (cur.left != null) {
            q.offer(cur.left);
        }
        if (cur.right != null) {
            q.offer(cur.right);
        }
    }
}

cpp 🤖

// 注意：cpp 代码由 chatGPT🤖 根据我的 java 代码翻译，旨在帮助不同背景的读者理解算法逻辑。
// 本代码不保证正确性，仅供参考。如有疑惑，可以参照我写的 java 代码对比查看。

// 输入一棵二叉树的根节点，遍历这棵二叉树所有节点
void levelTraverse(TreeNode* root) {
    if (root == nullptr) return 0;
    queue<TreeNode*> q;
    q.push(root);

    // 遍历二叉树的每一个节点
    while (!q.empty()) {
        TreeNode* cur = q.front();
        printf("我不知道节点 %s 在第几层", cur);

        // 将子节点放入队列
        if (cur->left != nullptr) {
            q.push(cur->left);
        }
        if (cur->right != nullptr) {
            q.push(cur->right);
        }
        q.pop();
    }
}

python 🤖

# 注意：python 代码由 chatGPT🤖 根据我的 java 代码翻译，旨在帮助不同背景的读者理解算法逻辑。
# 本代码不保证正确性，仅供参考。如有疑惑，可以参照我写的 java 代码对比查看。

# 输入一棵二叉树的根节点，遍历这棵二叉树所有节点
def levelTraverse(root: TreeNode) -> None:
    if not root:
        return 
    q = []
    q.append(root)

    # 遍历二叉树的每一个节点
    while q:
        cur = q.pop(0)
        print(f"我不知道节点 {cur} 在第几层")

        # 将子节点放入队列
        if cur.left:
            q.append(cur.left)
        if cur.right:
            q.append(cur.right)

go 🤖

// 注意：go 代码由 chatGPT🤖 根据我的 java 代码翻译，旨在帮助不同背景的读者理解算法逻辑。
// 本代码不保证正确性，仅供参考。如有疑惑，可以参照我写的 java 代码对比查看。

// 输入一棵二叉树的根节点，遍历这棵二叉树所有节点
func levelTraverse(root *TreeNode) {
    if root == nil {
        return
    }
    q := []*TreeNode{root}

    // 遍历二叉树的每一个节点
    for len(q) > 0 {
        cur := q[0]
        q = q[1:]
        printf("我不知道节点 %s 在第几层", cur)

        // 将子节点放入队列
        if cur.left != nil {
            q = append(q, cur.left)
        }
        if cur.right != nil {
            q = append(q, cur.right)
        }
    }
}

javascript 🤖

// 注意：javascript 代码由 chatGPT🤖 根据我的 java 代码翻译，旨在帮助不同背景的读者理解算法逻辑。
// 本代码不保证正确性，仅供参考。如有疑惑，可以参照我写的 java 代码对比查看。

function levelTraverse(root) {
  if (root == null) return 0;
  var q = [];
  q.push(root);

  while (q.length > 0) {
    var cur = q.shift();
    console.log("我不知道节点 " + cur + " 在第几层");

    if (cur.left != null) {
      q.push(cur.left);
    }
    if (cur.right != null) {
      q.push(cur.right);
    }
  }
}

但问题是，没有 for 循环，你也没办法维护 depth 变量了。

如果你想同时维护 depth 变量，让每个节点 cur 知道自己在第几层，可以想其他办法，比如新建一个 State 类，记录每个节点所在的层数：

java 🟢

class State {
    // 记录 node 节点的深度
    int depth;
    TreeNode node;

    State(TreeNode node, int depth) {
        this.depth = depth;
        this.node = node;
    }
}

// 输入一棵二叉树的根节点，遍历这棵二叉树所有节点
void levelTraverse(TreeNode root) {
    if (root == null) return 0;
    Queue<State> q = new LinkedList<>();
    q.offer(new State(root, 1));

    // 遍历二叉树的每一个节点
    while (!q.isEmpty()) {
        State cur = q.poll();
        TreeNode cur_node = cur.node;
        int cur_depth = cur.depth;
        printf("节点 %s 在第 %s 层", cur_node, cur_depth);

        // 将子节点放入队列
        if (cur_node.left != null) {
            q.offer(new State(cur_node.left, cur_depth + 1));
        }
        if (cur_node.right != null) {
            q.offer(new State(cur_node.right, cur_depth + 1));
        }
    }
}

cpp 🤖

// 注意：cpp 代码由 chatGPT🤖 根据我的 java 代码翻译，旨在帮助不同背景的读者理解算法逻辑。
// 本代码不保证正确性，仅供参考。如有疑惑，可以参照我写的 java 代码对比查看。

struct State {
    // 记录 node 节点的深度
    int depth;
    TreeNode* node;

    State(TreeNode* node, int depth) {
        this -> depth = depth;
        this -> node = node;
    }
};

// 输入一棵二叉树的根节点，遍历这棵二叉树所有节点
void levelTraverse(TreeNode* root) {
    if (root == nullptr) return;
    queue<State> q;
    q.push(State(root, 1));

    // 遍历二叉树的每一个节点
    while (!q.empty()) {
        State cur = q.front();
        q.pop();
        TreeNode* cur_node = cur.node;
        int cur_depth = cur.depth;
        printf("节点 %s 在第 %s 层", cur_node, cur_depth);

        // 将子节点放入队列
        if (cur_node -> left != nullptr) {
            q.push(State(cur_node -> left, cur_depth + 1));
        }
        if (cur_node -> right != nullptr) {
            q.push(State(cur_node -> right, cur_depth + 1));
        }
    }
}

python 🤖

# 注意：python 代码由 chatGPT🤖 根据我的 java 代码翻译，旨在帮助不同背景的读者理解算法逻辑。
# 本代码不保证正确性，仅供参考。如有疑惑，可以参照我写的 java 代码对比查看。

class State:
    def __init__(self, node: TreeNode, depth: int):
        self.depth = depth
        self.node = node

def levelTraverse(root: TreeNode) -> None:
    if not root:
        return 0
    q = []
    q.append(State(root, 1))

    while q:
        cur = q.pop(0)
        cur_node = cur.node
        cur_depth = cur.depth
        print(f"节点 {cur_node} 在第 {cur_depth} 层")

        if cur_node.left:
            q.append(State(cur_node.left, cur_depth + 1))
        if cur_node.right:
            q.append(State(cur_node.right, cur_depth + 1))

go 🤖

// 注意：go 代码由 chatGPT🤖 根据我的 java 代码翻译，旨在帮助不同背景的读者理解算法逻辑。
// 本代码不保证正确性，仅供参考。如有疑惑，可以参照我写的 java 代码对比查看。

type State struct { 
    depth int
    node *TreeNode
}

func levelTraverse(root *TreeNode) {
    if root == nil {
        return 0
    }
    q := make([]State, 0)
    q = append(q, State{root, 1})

    for len(q) > 0 {
        cur := q[0]
        q = q[1:]
        cur_node := cur.node
        cur_depth := cur.depth
        printf("节点 %s 在第 %s 层", cur_node, cur_depth)

        if cur_node.left != nil {
            q = append(q, State{cur_node.left, cur_depth + 1})
        }
        if cur_node.right != nil {
            q = append(q, State{cur_node.right, cur_depth + 1})
        }
    }
}

javascript 🤖

// 注意：javascript 代码由 chatGPT🤖 根据我的 java 代码翻译，旨在帮助不同背景的读者理解算法逻辑。
// 本代码不保证正确性，仅供参考。如有疑惑，可以参照我写的 java 代码对比查看。

var State = function(node, depth) {
    // 记录 node 节点的深度
    this.depth = depth;
    this.node = node;
};

// 输入一棵二叉树的根节点，遍历这棵二叉树所有节点
function levelTraverse(root) {
    if (root === null) return 0;
    var q = [];
    q.push(new State(root, 1));

    // 遍历二叉树的每一个节点
    while (q.length > 0) {
        var cur = q.shift();
        var cur_node = cur.node;
        var cur_depth = cur.depth;
        console.log("节点 " + cur_node + " 在第 " + cur_depth + " 层");

        // 将子节点放入队列
        if (cur_node.left != null) {
            q.push(new State(cur_node.left, cur_depth + 1));
        }
        if (cur_node.right != null) {
            q.push(new State(cur_node.right, cur_depth + 1));
        }
    }
}

这样，我们就可以不使用 for 循环也确切地知道每个二叉树节点的深度了。

如果你能够理解上面这段代码，我们就可以来看 Dijkstra 算法的代码框架了。

加载中...