拓展：如何计算完全二叉树的节点数

labuladong原创数据结构二叉树约 1214 字

Info

已完成网站教程、网站习题、配套插件中所有多语言代码的校准，解决了之前 chatGPT 翻译可能出错的问题~

读完本文，你不仅学会了算法套路，还可以顺便解决如下题目：

LeetCode	力扣	难度
222. Count Complete Tree Nodes	222. 完全二叉树的节点个数	🟠

前置知识

阅读本文前，你需要先学习：

如果让你数一下一棵普通二叉树有多少个节点，这很简单，只要在二叉树的遍历框架上加一点代码就行了。

但是，力扣第第 222 题「完全二叉树的节点个数」给你一棵完全二叉树，让你计算它的节点个数，你会不会？算法的时间复杂度是多少？

这个算法的时间复杂度应该是 O(logN*logN)，如果你心中的算法没有达到这么高效，那么本文就是给你写的。

关于「完全二叉树」和「满二叉树」等名词的定义，可以参考基础知识章节的二叉树基础。

一、思路分析

现在回归正题，如何求一棵完全二叉树的节点个数呢？

java 🟢

// 输入一棵完全二叉树，返回节点总数
int countNodes(TreeNode root);

cpp 🤖

// 输入一棵完全二叉树，返回节点总数
int countNodes(TreeNode* root);

python 🤖

# 输入一棵完全二叉树，返回节点总数
def countNodes(root: TreeNode) -> int:

go 🤖

// 输入一棵完全二叉树，返回节点总数
func countNodes(root *TreeNode) int {
}

javascript 🤖

// 输入一棵完全二叉树，返回节点总数
var countNodes = function(root) {}

如果是一个普通二叉树，显然只要向下面这样遍历一边即可，时间复杂度 O(N)：

java 🟢

public int countNodes(TreeNode root) {
    if (root == null) return 0;
    return 1 + countNodes(root.left) + countNodes(root.right);
}

cpp 🤖

int countNodes(TreeNode* root) {
    if (root == nullptr) return 0;
    return 1 + countNodes(root->left) + countNodes(root->right);
}

python 🤖

def countNodes(root: TreeNode) -> int:
    if root == None:
        return 0
    return 1 + countNodes(root.left) + countNodes(root.right)

go 🤖

func countNodes(root *TreeNode) int {
    if root == nil {
        return 0
    }
    return 1 + countNodes(root.Left) + countNodes(root.Right)
}

javascript 🤖

var countNodes = function(root) {
    if (root === null) return 0;
    return 1 + countNodes(root.left) + countNodes(root.right);
};

那如果是一棵满二叉树，节点总数就和树的高度呈指数关系：

java 🟢

public int countNodes(TreeNode root) {
    int h = 0;
    // 计算树的高度
    while (root != null) {
        root = root.left;
        h++;
    }
    // 节点总数就是 2^h - 1
    return (int)Math.pow(2, h) - 1;
}

cpp 🤖

int countNodes(TreeNode* root) {
    int h = 0;
    // 计算树的高度
    while (root != nullptr) {
        root = root->left;
        h++;
    }
    // 节点总数就是 2^h - 1
    return pow(2, h) - 1;
}

python 🤖

def countNodes(root: TreeNode) -> int:
    h = 0
    # 计算树的高度
    while root:
        root = root.left
        h += 1
    # 节点总数就是 2^h - 1
    return 2 ** h - 1

go 🤖

func countNodes(root *TreeNode) int {
    h := 0
    // 计算树的高度
    for root != nil {
        root = root.Left
        h++
    }
    // 节点总数就是 2^h - 1
    return int(math.Pow(2, float64(h))) - 1
}

javascript 🤖

var countNodes = function(root) {
    var h = 0;
    
    // 计算树的高度
    while (root !== null) {
        root = root.left;
        h++;
    }
    
    // 节点总数就是 2^h - 1
    return Math.pow(2, h) - 1;
};

完全二叉树比普通二叉树特殊，但又没有满二叉树那么特殊，计算它的节点总数，可以说是普通二叉树和完全二叉树的结合版，先看代码：

java 🟢

class Solution {
    public int countNodes(TreeNode root) {
        TreeNode l = root, r = root;
        // 沿最左侧和最右侧分别计算高度
        int hl = 0, hr = 0;
        while (l != null) {
            l = l.left;
            hl++;
        }
        while (r != null) {
            r = r.right;
            hr++;
        }
        // 如果左右侧计算的高度相同，则是一棵满二叉树
        if (hl == hr) {
            return (int)Math.pow(2, hl) - 1;
        }
        // 如果左右侧的高度不同，则按照普通二叉树的逻辑计算
        return 1 + countNodes(root.left) + countNodes(root.right);
    }
}

cpp 🤖

class Solution {
public:
    int countNodes(TreeNode* root) {
        TreeNode* l = root, * r = root;
        // 沿最左侧和最右侧分别计算高度
        int hl = 0, hr = 0;
        while (l != nullptr) {
            l = l->left;
            hl++;
        }
        while (r != nullptr) {
            r = r->right;
            hr++;
        }
        // 如果左右侧计算的高度相同，则是一棵满二叉树
        if (hl == hr) {
            return pow(2, hl) - 1;
        }
        // 如果左右侧的高度不同，则按照普通二叉树的逻辑计算
        return 1 + countNodes(root->left) + countNodes(root->right);
    }
};

python 🤖

class Solution:
    def countNodes(self, root: TreeNode) -> int:
        l = root
        r = root
        hl = 0
        hr = 0
        # 沿最左侧和最右侧分别计算高度
        while l is not None:
            l = l.left
            hl += 1
        while r is not None:
            r = r.right
            hr += 1
        # 如果左右侧计算的高度相同，则是一棵满二叉树
        if hl == hr:
            return pow(2, hl) - 1
        # 如果左右侧的高度不同，则按照普通二叉树的逻辑计算
        return 1 + self.countNodes(root.left) + self.countNodes(root.right)

go 🤖

func countNodes(root *TreeNode) int {
    l, r := root, root
    // 沿最左侧和最右侧分别计算高度
    hl, hr := 0, 0
    for l != nil {
        l = l.Left
        hl++
    }
    for r != nil {
        r = r.Right
        hr++
    }
    // 如果左右侧计算的高度相同，则是一棵满二叉树
    if hl == hr {
        return int(math.Pow(2, float64(hl))) - 1
    }
    // 如果左右侧的高度不同，则按照普通二叉树的逻辑计算
    return 1 + countNodes(root.Left) + countNodes(root.Right)
}

javascript 🤖

var countNodes = function(root) {
    let l = root, r = root;
    // 沿最左侧和最右侧分别计算高度
    let hl = 0, hr = 0;
    while (l !== null) {
        l = l.left;
        hl++;
    }
    while (r !== null) {
        r = r.right;
        hr++;
    }
    // 如果左右侧计算的高度相同，则是一棵满二叉树
    if (hl === hr) {
        return Math.pow(2, hl) - 1;
    }
    // 如果左右侧的高度不同，则按照普通二叉树的逻辑计算
    return 1 + countNodes(root.left) + countNodes(root.right);
};

结合刚才针对满二叉树和普通二叉树的算法，上面这段代码应该不难理解，就是一个结合版，但是其中降低时间复杂度的技巧是非常微妙的。

二、复杂度分析

开头说了，这个算法的时间复杂度是 O(logN*logN)，这是怎么算出来的呢？

直觉感觉好像最坏情况下是 O(N*logN) 吧，因为之前的 while 需要 logN 的时间，最后要 O(N) 的时间向左右子树递归：

return 1 + countNodes(root.left) + countNodes(root.right);

关键点在于，这两个递归只有一个会真的递归下去，另一个一定会触发 hl == hr 而立即返回，不会递归下去。

为什么呢？原因如下：

一棵完全二叉树的两棵子树，至少有一棵是满二叉树：

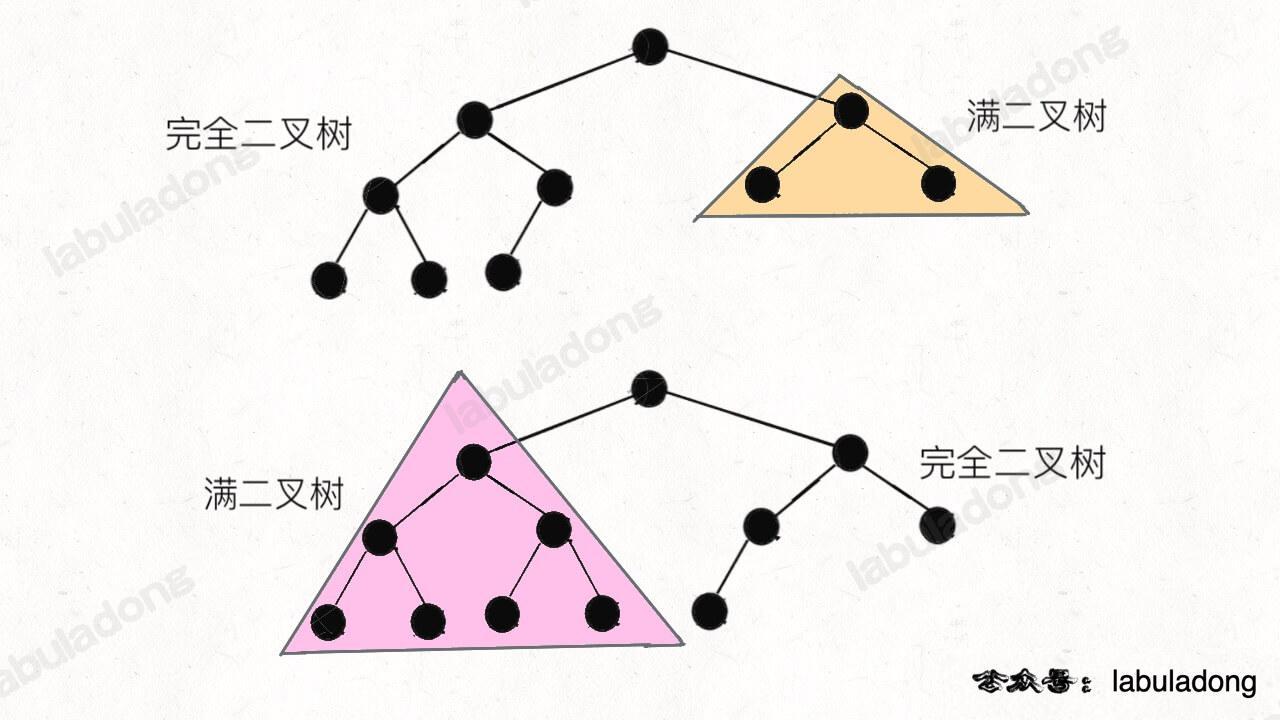
看图就明显了吧，由于完全二叉树的性质，其子树一定有一棵是满的，所以一定会触发 hl == hr，只消耗 O(logN) 的复杂度而不会继续递归。

综上，算法的递归深度就是树的高度 O(logN)，每次递归所花费的时间就是 while 循环，需要 O(logN)，所以总体的时间复杂度是 O(logN*logN)。

所以说，「完全二叉树」这个概念还是有它存在的原因的，不仅适用于数组实现二叉堆，而且连计算节点总数这种看起来简单的操作都有高效的算法实现。

拓展：如何计算完全二叉树的节点数

222. 完全二叉树的节点个数 https://leetcode.cn/problems/count-complete-tree-nodes

222. Count Complete Tree Nodes https://leetcode.com/problems/count-complete-tree-nodes

一、思路分析

二、复杂度分析