前文 哈希表核心原理 中我介绍了哈希表的核心原理和几个关键概念,其中提到了解决哈希冲突的方法主要有两种,分别是拉链法和线性探查法(也常叫做开放寻址法):
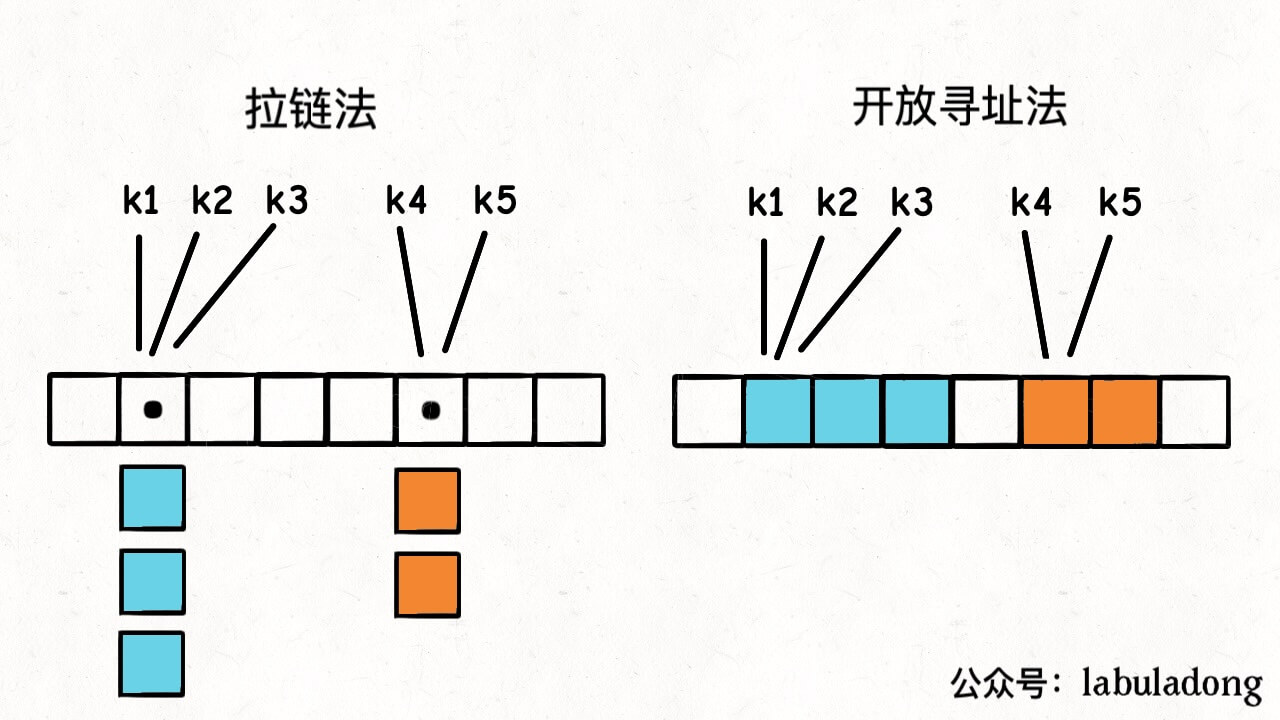
由于线性探查法稍微复杂一些,本文先讲解实现线性探查法的几个难点,下篇文章再给出具体的代码实现。
简化场景
之前介绍的拉链法应该是比较简单的,无非就是 table 中每个元素都是一个链表,出现哈希冲突的话往链表里塞元素就行了。
而线性探查法会更复杂,主要有两个难点,涉及到多种数组操作技巧。在讲清楚这两个难点之前,我们先设定一个简化的场景:
假设我们的哈希表只支持 key 类型为 int,value 类型为 int 的情况,且 table.length 固定为 10,hash 函数的实现是 hash(key) = key % 10。因为这样比较容易模拟出哈希冲突,比如 hash(1) 和 hash(11) 的值都是 1。
线性探查法的大致逻辑如下:
// 线性探查法的基本逻辑,伪码实现
class MyLinearProbingHashMap {
// 数组中每个元素都存储一个键值对
private KVNode[] table = new KVNode[5];
private int hash(int key) {
return key % table.length;
}
public void put(int key, int value) {
int index = hash(key);
KVNode node = table[index];
if (node == null) {
table[index] = new KVNode(key, value);
} else {
// 线性探查法的逻辑
// 向后探查,直到找到 key 或者找到空位
while (table[index] != null && table[index].key != key) {
index++
}
table[index] = new KVNode(key, value);
}
}
public int get(int key) {
int index = hash(key);
// 向后探查,直到找到 key 或者找到空位
while (table[index] != null && table[index].key != key) {
index++;
}
if (table[index] == null) {
return -1;
}
return table[index].value;
}
public void remove(int key) {
int index = hash(key);
// 向后探查,直到找到 key 或者找到空位
while (table[index] != null && table[index].key != key) {
index++;
}
// 删除 table[index]
// ...
}
}基于这个假设场景,我们来看看线性探查法的两个难点。
难点一:需要环形数组技巧
在线性探查的过程中,可能需要用到之前讲过的 环形数组技巧。
我们底层的 table 数组是一个一维数组,当发生哈希冲突时,我们需要往后找一个空位。如果一直找到数组的末尾还没找到空位,怎么办?这时候就需要转到数组的头部继续找空位,直到找到为止。
这种场景就得靠前文讲的环形数组技巧来实现。
举个具体点的例子,比方说调用一次 put(8, a),底层 table 数组的情况是这样的:
table = [_, _, ..., _, a, _]
index 0 1 ... 7 8 9再调用一次 put(18, b),发现 hash(18) = 8 这个索引已经被占用了,那么就往后找一个空位:
table = [_, _, ..., _, a, b]
index 0 1 ... 7 8 9如果再调用一次 put(28, c),发现 hash(28) = 8 这个索引还是被占用了,那么就继续往后找空位,找到最后一个位置还没找到,就要转到数组的头部继续找:
table = [c, _, ..., _, a, b]
index 0 1 ... 7 8 9这是 put 方法添加元素时的情况,在查找和删除元素的时候,也会遇到类似的问题,这里就不多说了。
难点二:删除操作较复杂
线性探查法的删除操作比较复杂,因为要维护元素的连续性。
就好比我们之前实现的 动态数组,因为要维护元素的连续性,所以删除和插入元素都比较麻烦。
为什么线性探查法也要维护元素的连续性呢,比方说我这样调用:
put(0, a)
put(10, b)
put(20, c)
put(3, A)
put(13, B)
put(30, d)
put(40, e)那么底层 table 数组的情况是这样的:
table = [a, b, c, A, B, d, e, _, _, _]
index 0 1 2 3 4 5 6 7 8 9
hash ^ ^
key 0 10 20 3 13 30 40比方说,现在你想删除 key = 10 这个键值对,怎么办?如果你直接把 table[1] 置为 null,就会变成这样:
table = [a, _, c, A, B, d, e, _, _, _]
index 0 1 2 3 4 5 6 7 8 9
hash ^ ^
key 0 20 3 13 30 40这样一来元素就不连续了,回顾一下 get 方法的逻辑,此时调用 get(20), get(30), get(40) 的时候就会发现找不到对应 key,这是错误的,哈希表被搞坏了。
何解?有两种方法,我一个一个来讲。
方法一:数据搬移避免空洞
在 table 中删除元素时,可以进行类似数组的数据搬移操作,把后面的元素往前挪,保证元素的连续性。
但这里的搬移操作其实比数组的搬移操作更复杂,因为你不能把 table[1] 后面的全部元素往前挪,而应该仅挪动在索引 0 出现哈希冲突的元素。
举例来说,你如果移动后面的所有元素,table 就会变成这样:
table = [a, c, A, B, d, e, _, _, _, _]
index 0 1 2 3 4 5 6 7 8 9
hash ^ ^
key 0 20 3 13 30 40看到问题了么?key = 3, value = A 的那个键值对你还能找到么?不能,hash(3) = 3,顺着 table[3] 往后一直找都找不到,因为它被错误地往前移动了。
正确的做法是,只把在 hash(key) = 0 出现哈希冲突的元素往前挪,其他元素要不动,这样才能保证线性探查的正确性。
也就是说,删除 key = 10 之后,table 应该变成这样:
table = [a, c, d, A, B, e, _, _, _, _]
index 0 1 2 3 4 5 6 7 8 9
hash ^ ^
key 0 20 30 3 13 40这样一来,获取每个 key 对应的 value 就不会出错了。
但是如何能够精确地移动元素呢?这就需要一些技巧了,下篇文章会给出代码实现,这里你可以先自己思考一下。
方法二:占位符标记删除
还有一种方法,就是通过一个特殊值作为占位符来标记被删元素,这样就可以避免数据搬移,同时保证元素连续。
还是这个例子:
table = [a, b, c, A, B, d, e, _, _, _]
index 0 1 2 3 4 5 6 7 8 9
hash ^ ^
key 0 10 20 3 13 30 40如果你想删除 key = 10,那么你可以把 table[1] 设置为一个特殊占位符标记为删除,我用 x 来表示,这样 table 就变成了:
table = [a, x, c, A, B, d, e, _, _, _]
index 0 1 2 3 4 5 6 7 8 9
hash ^ ^
key 0 20 3 13 30 40在 get 方法中会特殊处理这个特殊值,所以你调用 get(10) 的时候会返回 -1,表示没有找到。
同时,你调用 get(20), get(30), get(40) 的时候,还是可以正确地向后找到对应的 value。
这种方法的好处是,不需要进行数据搬移,删除操作处理起来比较简单。
但也有缺点,比如如果你不断地插入和删除元素,table 数组中会出现很多这样占位符,这样会增加连续元素的长度,进而降低 get 方法线性探查的效率。
而且还有一种很 tricky 的情况,比如你不断插入和删除元素,导致 table 中全部都是占位符。如果你不对这种情况进行特殊处理,那么此时你调用一次 get 方法,由于环形数组的特性,算法就会陷入死循环。
这里就提一下,具体实现可以看后面我给出的代码。
总结
上面讲到了线性探查法的两个难点,你感觉怎么样?是不是还没看到代码,就觉得线性探查法比拉链法复杂多了?
所以线性探查法使用得不多,大部分编程语言标准库实现的哈希表都是用拉链法,因为它更简单不容易出错,而且正如我在 哈希表原理 中提到的,拉链法可以支持无限大的负载因子,而线性探查法不行。
数据结构这个东西是拿来用的,而不是拿来秀的,并不是越复杂越好,简单实用、易学易维护才是王道。
所以线性探查法仅做了解即可,具体代码和算法可视化我会放到下一篇文章。