Two Pointer Techniques for Linked List Problems
Note
Now all the plugins has supported English. I'm still improving the website...
This article will resolve
Prerequisites
Before reading this article, you should first learn:
This article summarizes basic techniques for singly linked lists, with each technique corresponding to at least one algorithm problem:
- Merging Two Sorted Linked Lists
- Splitting a Linked List
- Merging
kSorted Linked Lists - Finding the
k-th Node from the End of a Singly Linked List - Finding the Middle Node of a Singly Linked List
- Detecting a Cycle in a Singly Linked List and Finding the Start of the Cycle
- Determining if Two Singly Linked Lists Intersect and Finding the Intersection Node
These solutions all use the double pointer technique, which is very widely used for singly linked list problems. Let's go through them one by one.
Merging Two Sorted Linked Lists
This is the most basic linked list technique. LeetCode problem 21, "Merge Two Sorted Linked Lists," addresses this issue. You are given two sorted linked lists and asked to merge them into a new sorted linked list:
21. Merge Two Sorted Lists | LeetCode |
You are given the heads of two sorted linked lists list1 and list2.
Merge the two lists into one sorted list. The list should be made by splicing together the nodes of the first two lists.
Return the head of the merged linked list.
Example 1:
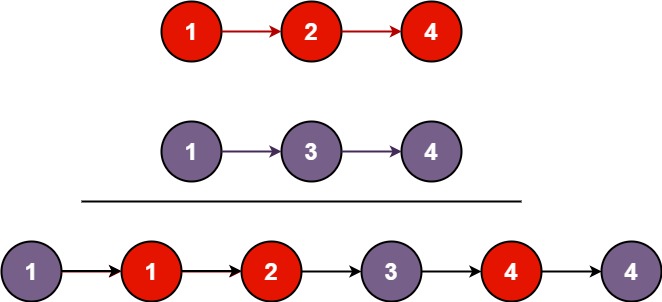
Input: list1 = [1,2,4], list2 = [1,3,4] Output: [1,1,2,3,4,4]
Example 2:
Input: list1 = [], list2 = [] Output: []
Example 3:
Input: list1 = [], list2 = [0] Output: [0]
Constraints:
- The number of nodes in both lists is in the range
[0, 50]. -100 <= Node.val <= 100- Both
list1andlist2are sorted in non-decreasing order.
// The function signature is as follows
ListNode mergeTwoLists(ListNode l1, ListNode l2);// The function signature is as follows
ListNode* mergeTwoLists(ListNode* l1, ListNode* l2);# The function signature is as follows
def mergeTwoLists(l1: ListNode, l2: ListNode) -> ListNode:// The function signature is as follows
func mergeTwoLists(l1 *ListNode, l2 *ListNode) *ListNode {}// the function signature is as follows
var mergeTwoLists = function(l1, l2) {}This problem is quite simple. Let's directly look at the solution:
class Solution {
public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
// virtual head node
ListNode dummy = new ListNode(-1), p = dummy;
ListNode p1 = l1, p2 = l2;
while (p1 != null && p2 != null) {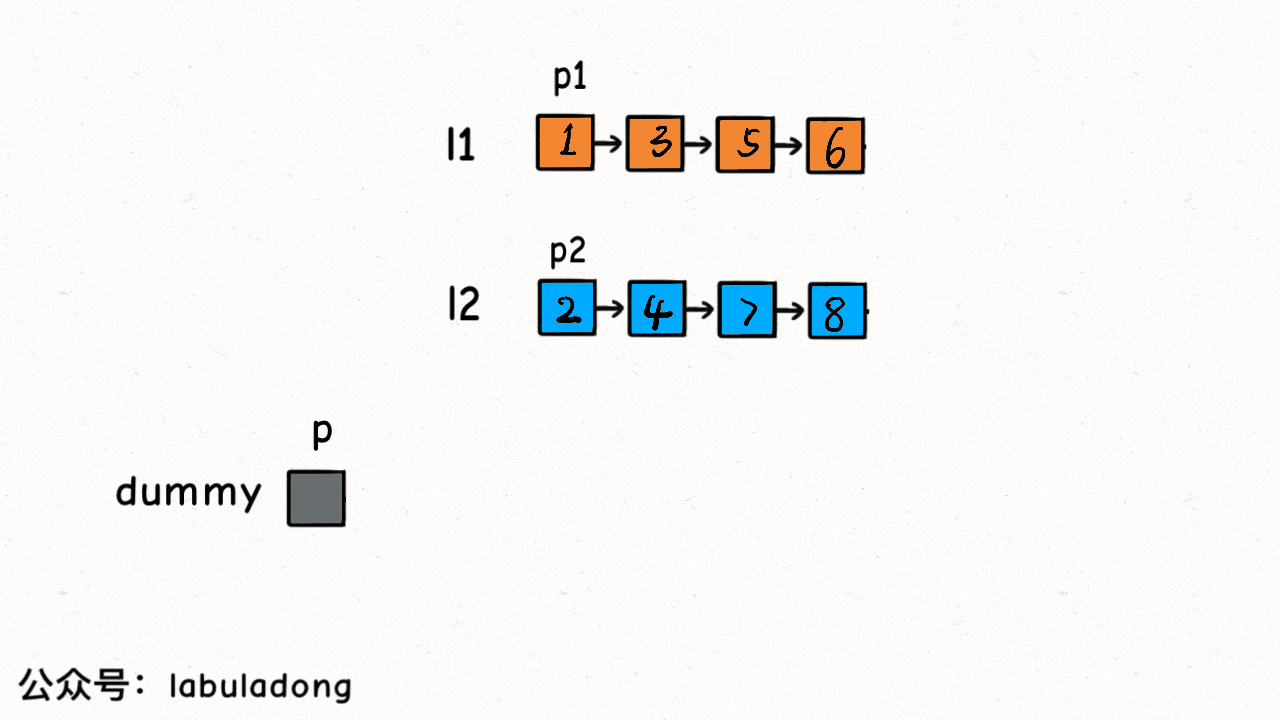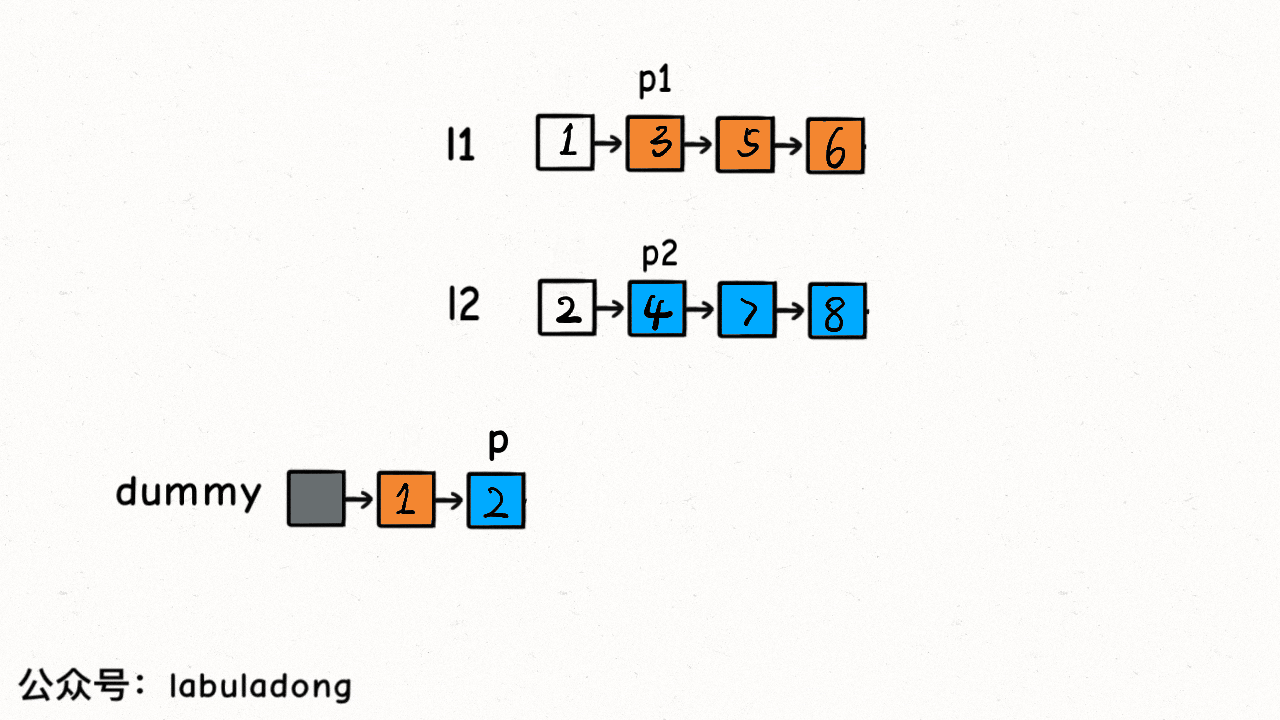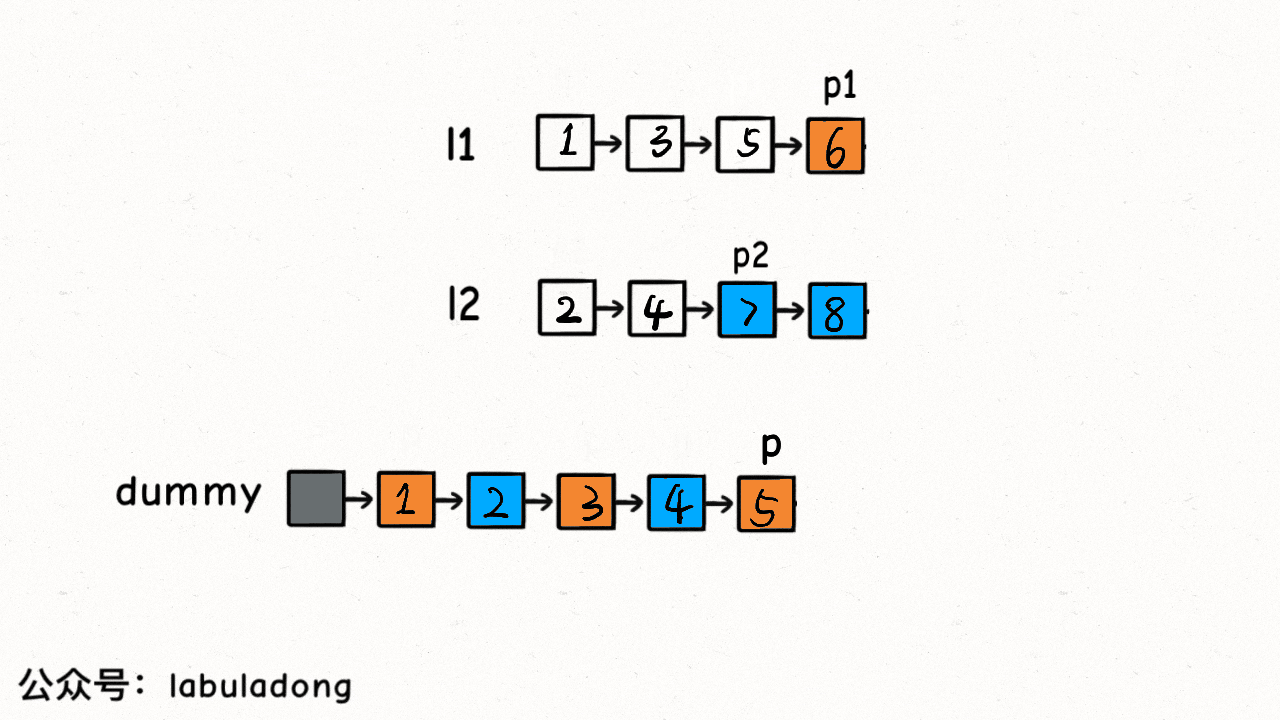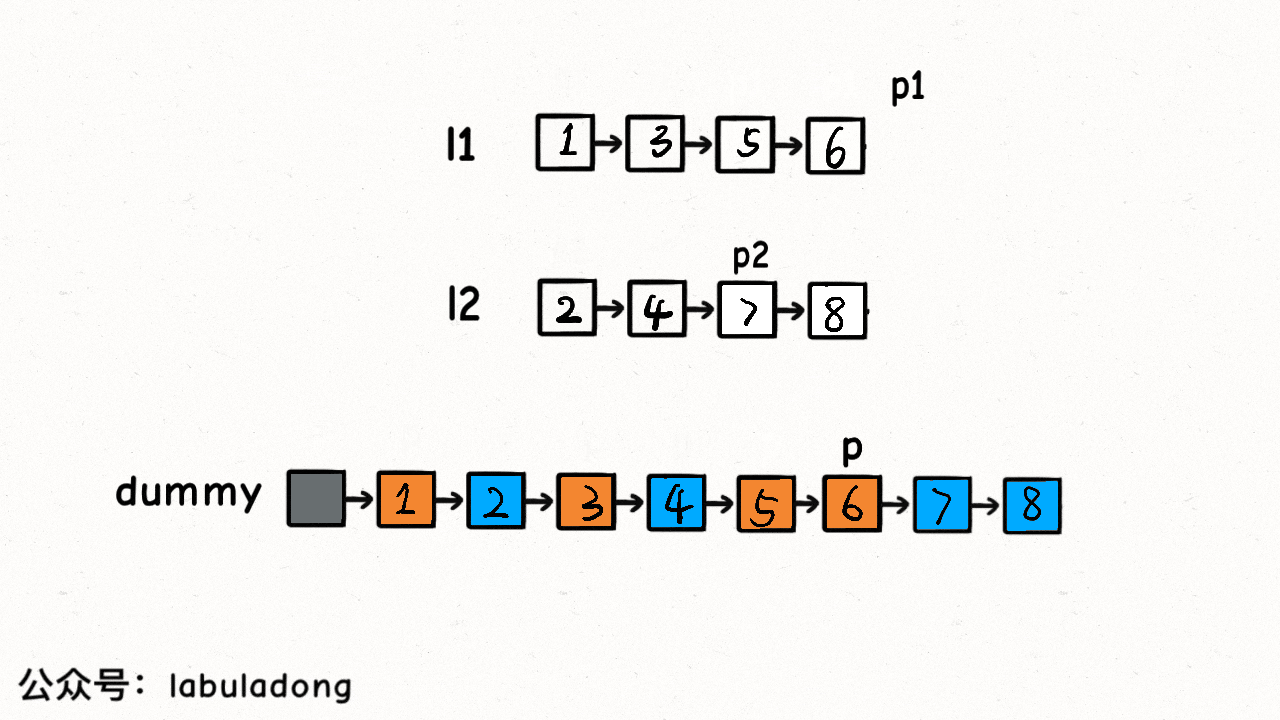
// compare pointers p1 and p2
// attach the node with the smaller value to the p pointer
if (p1.val > p2.val) {
p.next = p2;
p2 = p2.next;
} else {
p.next = p1;
p1 = p1.next;
}
// advance the p pointer
p = p.next;
}
if (p1 != null) {
p.next = p1;
}
if (p2 != null) {
p.next = p2;
}
return dummy.next;
}
}class Solution {
public:
ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {
// dummy head node
ListNode dummy(-1), *p = &dummy;
ListNode *p1 = l1, *p2 = l2;
while (p1 != nullptr && p2 != nullptr) {
// compare the two pointers p1 and p2
// attach the node with the smaller value to the pointer p
if (p1->val > p2->val) {
p->next = p2;
p2 = p2->next;
} else {
p->next = p1;
p1 = p1->next;
}
// advance the pointer p continuously
p = p->next;
}
if (p1 != nullptr) {
p->next = p1;
}
if (p2 != nullptr) {
p->next = p2;
}
return dummy.next;
}
};class Solution:
def mergeTwoLists(self, l1: ListNode, l2: ListNode) -> ListNode:
# dummy head node
dummy = ListNode(-1)
p = dummy
p1 = l1
p2 = l2
while p1 is not None and p2 is not None:
# compare the two pointers p1 and p2
# attach the node with the smaller value to the p pointer
if p1.val > p2.val:
p.next = p2
p2 = p2.next
else:
p.next = p1
p1 = p1.next
# the p pointer keeps moving forward
p = p.next
if p1 is not None:
p.next = p1
if p2 is not None:
p.next = p2
return dummy.nextfunc mergeTwoLists(l1 *ListNode, l2 *ListNode) *ListNode {
// dummy head node
dummy := &ListNode{-1, nil}
p := dummy
p1 := l1
p2 := l2
for p1 != nil && p2 != nil {
// compare pointers p1 and p2
// attach the node with the smaller value to the p pointer
if p1.Val > p2.Val {
p.Next = p2
p2 = p2.Next
} else {
p.Next = p1
p1 = p1.Next
}
// advance the p pointer
p = p.Next
}
if p1 != nil {
p.Next = p1
}
if p2 != nil {
p.Next = p2
}
return dummy.Next
}var mergeTwoLists = function(l1, l2) {
// virtual head node
var dummy = new ListNode(-1), p = dummy;
var p1 = l1, p2 = l2;
while (p1 !== null && p2 !== null) {
// compare the two pointers p1 and p2
// attach the node with the smaller value to the pointer p
if (p1.val > p2.val) {
p.next = p2;
p2 = p2.next;
} else {
p.next = p1;
p1 = p1.next;
}
// the p pointer keeps moving forward
p = p.next;
}
if (p1 !== null) {
p.next = p1;
}
if (p2 !== null) {
p.next = p2;
}
return dummy.next;
};In our while loop, we compare the sizes of p1 and p2 each time, attaching the smaller node to the result list. Refer to the GIF below:
To visually understand, the logic of this algorithm is similar to zipping up a zipper, where l1 and l2 are like the teeth on either side of the zipper, and the pointer p acts like the slider, merging the two sorted linked lists. Alternatively, you can think of this process like protein synthesis, where l1 and l2 resemble amino acids, and the pointer p functions like the enzyme, linking the amino acids into proteins.
The code also employs a common technique in linked list problems known as the "dummy head node" or dummy node. You can test it out; without using a dummy node, the code becomes more complex, requiring extra handling for when pointer p is null. The dummy node serves as a placeholder, simplifying the code by avoiding null pointer scenarios.
Tips
Readers often ask, when should one use a dummy head node? Here's a summary: When you need to create a new linked list, using a dummy head node can simplify handling edge cases.
For instance, when merging two sorted linked lists into a new sorted linked list, aren’t you creating a new list? Or when you want to split a linked list into two, aren’t you also creating new lists? In these situations, a dummy head node can help simplify edge case management.
Decomposing a Singly Linked List
Let's directly look at LeetCode Problem 86 "Partition List":
86. Partition List | LeetCode |
Given the head of a linked list and a value x, partition it such that all nodes less than x come before nodes greater than or equal to x.
You should preserve the original relative order of the nodes in each of the two partitions.
Example 1:
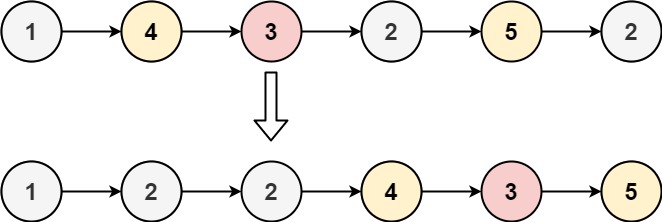
Input: head = [1,4,3,2,5,2], x = 3 Output: [1,2,2,4,3,5]
Example 2:
Input: head = [2,1], x = 2 Output: [1,2]
Constraints:
- The number of nodes in the list is in the range
[0, 200]. -100 <= Node.val <= 100-200 <= x <= 200
When merging two sorted linked lists, you combine them into one. Here, you need to decompose the original list into two. Specifically, we can split the original list into two smaller lists, with one containing elements less than x, and the other containing elements greater than or equal to x. Finally, by connecting these two lists together, you achieve the desired outcome.
The overall logic is very similar to merging sorted linked lists. Let's look at the code for details, and pay attention to the use of the dummy head node:
class Solution {
public ListNode partition(ListNode head, int x) {
// dummy head node for the list containing nodes less than x
ListNode dummy1 = new ListNode(-1);
// dummy head node for the list containing nodes greater than or equal to x
ListNode dummy2 = new ListNode(-1);
// p1, p2 pointers are responsible for creating the result list
ListNode p1 = dummy1, p2 = dummy2;
// p is responsible for traversing the original list, similar to the logic of merging two sorted lists
// here we are splitting one list into two lists
ListNode p = head;
while (p != null) {
if (p.val >= x) {
p2.next = p;
p2 = p2.next;
} else {
p1.next = p;
p1 = p1.next;
}
// we cannot move p pointer directly,
// p = p.next
// disconnect the next pointer of each node in the original list
ListNode temp = p.next;
p.next = null;
p = temp;
}
// connect the two lists
p1.next = dummy2.next;
return dummy1.next;
}
}class Solution {
public:
ListNode* partition(ListNode* head, int x) {
// virtual head node for the list storing nodes less than x
ListNode* dummy1 = new ListNode(-1);
// virtual head node for the list storing nodes greater than or equal to x
ListNode* dummy2 = new ListNode(-1);
// p1, p2 pointers responsible for generating the result list
ListNode* p1 = dummy1, *p2 = dummy2;
// p is responsible for traversing the original list, similar to the logic of merging two sorted lists
// here we decompose a list into two lists
ListNode* p = head;
while (p != nullptr) {
if (p->val >= x) {
p2->next = p;
p2 = p2->next;
} else {
p1->next = p;
p1 = p1->next;
}
// cannot directly advance the p pointer,
// p = p->next
// disconnect the next pointer of each node in the original list
ListNode* temp = p->next;
p->next = nullptr;
p = temp;
}
// connect the two lists
p1->next = dummy2->next;
return dummy1->next;
}
};class Solution:
def partition(self, head: ListNode, x: int) -> ListNode:
# virtual head node for the list containing elements less than x
dummy1 = ListNode(-1)
# virtual head node for the list containing elements greater than or equal to x
dummy2 = ListNode(-1)
# p1, p2 pointers are responsible for creating the resulting list
p1, p2 = dummy1, dummy2
# p is responsible for traversing the original list, similar to the logic of merging two sorted lists
# here we decompose one list into two lists
p = head
while p:
if p.val >= x:
p2.next = p
p2 = p2.next
else:
p1.next = p
p1 = p1.next
# cannot directly move the p pointer forward,
# p = p.next
# break the next pointer of each node in the original list
temp = p.next
p.next = None
p = temp
# connect the two lists
p1.next = dummy2.next
return dummy1.nextfunc partition(head *ListNode, x int) *ListNode {
// virtual head node for the list storing nodes less than x
dummy1 := &ListNode{-1, nil}
// virtual head node for the list storing nodes greater than or equal to x
dummy2 := &ListNode{-1, nil}
// pointers p1 and p2 are responsible for generating the result list
p1, p2 := dummy1, dummy2
// pointer p is responsible for traversing the original list, similar to merging two sorted lists
// here we split one list into two lists
p := head
for p != nil {
if p.Val >= x {
p2.Next = p
p2 = p2.Next
} else {
p1.Next = p
p1 = p1.Next
}
// cannot move the p pointer forward directly,
// p = p.Next
// break the next pointer of each node in the original list
temp := p.Next
p.Next = nil
p = temp
}
// connect the two lists
p1.Next = dummy2.Next
return dummy1.Next
}var partition = function(head, x) {
// dummy head node for the list with nodes less than x
let dummy1 = new ListNode(-1);
// dummy head node for the list with nodes greater than or equal to x
let dummy2 = new ListNode(-1);
// p1 and p2 pointers are responsible for creating the result lists
let p1 = dummy1, p2 = dummy2;
// p is responsible for traversing the original list, similar to the logic of merging two sorted lists
// here we split the list into two lists
let p = head;
while (p !== null) {
if (p.val >= x) {
p2.next = p;
p2 = p2.next;
} else {
p1.next = p;
p1 = p1.next;
}
// cannot directly advance the p pointer,
// p = p.next
// break the next pointer of each node in the original list
let temp = p.next;
p.next = null;
p = temp;
}
// connect the two lists
p1.next = dummy2.next;
return dummy1.next;
};I know many readers might have questions about this piece of code:
// Can't move the p pointer forward directly,
// p = p.next
// Break the next pointer of each node in the original linked list
ListNode temp = p.next;
p.next = null;
p = temp;Let's get straight to the point with our visual panel to understand it better. First, here's the correct way to do it:
If you don't disconnect the next pointer of each node in the original linked list, an error will occur because the resulting linked list will contain a cycle:
In general, if we need to attach nodes from the original linked list to a new linked list instead of creating new nodes, it might be necessary to disconnect the links between the nodes and the original list. This can be a good habit to develop: whenever you encounter such a situation, break the connection of the original linked list nodes to avoid errors.
Merging k Sorted Linked Lists
Let's look at LeetCode Problem 23 "Merge k Sorted Lists":
23. Merge k Sorted Lists | LeetCode |
You are given an array of k linked-lists lists, each linked-list is sorted in ascending order.
Merge all the linked-lists into one sorted linked-list and return it.
Example 1:
Input: lists = [[1,4,5],[1,3,4],[2,6]] Output: [1,1,2,3,4,4,5,6] Explanation: The linked-lists are: [ 1->4->5, 1->3->4, 2->6 ] merging them into one sorted list: 1->1->2->3->4->4->5->6
Example 2:
Input: lists = [] Output: []
Example 3:
Input: lists = [[]] Output: []
Constraints:
k == lists.length0 <= k <= 1040 <= lists[i].length <= 500-104 <= lists[i][j] <= 104lists[i]is sorted in ascending order.- The sum of
lists[i].lengthwill not exceed104.
// The function signature is as follows
ListNode mergeKLists(ListNode[] lists);// The function signature is as follows
ListNode* mergeKLists(vector<ListNode*>& lists);# The function signature is as follows
def mergeKLists(lists: List[ListNode]) -> ListNode:// The function signature is as follows
func mergeKLists(lists []*ListNode) *ListNode// The function signature is as follows
var mergeKLists = function(lists) {};Merging k sorted linked lists is similar to merging two sorted linked lists. The challenge is how to quickly get the smallest node among the k nodes and attach it to the result linked list.
Here, we need to use a priority queue data structure. By putting the linked list nodes into a min-heap, we can get the smallest node among the k nodes each time. For more details on priority queues, you can refer to Priority Queue (Binary Heap) Principles and Implementation. This article will not go into that.
class Solution {
public ListNode mergeKLists(ListNode[] lists) {
if (lists.length == 0) return null;
// virtual head node
ListNode dummy = new ListNode(-1);
ListNode p = dummy;
// priority queue, min-heap
PriorityQueue<ListNode> pq = new PriorityQueue<>(
lists.length, (a, b)->(a.val - b.val));
// add the head nodes of the k linked lists to the min-heap
for (ListNode head : lists) {
if (head != null) {
pq.add(head);
}
}
while (!pq.isEmpty()) {
// get the smallest node and attach it to the result linked list
ListNode node = pq.poll();
p.next = node;
if (node.next != null) {
pq.add(node.next);
}
// p pointer keeps moving forward
p = p.next;
}
return dummy.next;
}
}class Solution {
public:
ListNode* mergeKLists(vector<ListNode*>& lists) {
if (lists.empty()) return nullptr;
// dummy head node
ListNode* dummy = new ListNode(-1);
ListNode* p = dummy;
// priority queue, min-heap
auto cmp = [](ListNode* a, ListNode* b) { return a->val > b->val; };
priority_queue<ListNode*, vector<ListNode*>, decltype(cmp)> pq(cmp);
// add the head nodes of k linked lists to the min-heap
for (ListNode* head : lists) {
if (head != nullptr) {
pq.push(head);
}
}
while (!pq.empty()) {
// get the smallest node and attach it to the result linked list
ListNode* node = pq.top();
pq.pop();
p->next = node;
if (node->next != nullptr) {
pq.push(node->next);
}
// move the p pointer forward continuously
p = p->next;
}
return dummy->next;
}
};import heapq
class ListNode:
def __init__(self, val=0, next=None):
self.val = val
self.next = next
# Override comparison operators to facilitate adding ListNode to the min-heap
def __lt__(self, other):
return self.val < other.val
class Solution:
def mergeKLists(self, lists):
if not lists:
return None
# Dummy head node
dummy = ListNode(-1)
p = dummy
# Priority queue, min-heap
pq = []
# Add the head nodes of k linked lists to the min-heap
for i, head in enumerate(lists):
if head is not None:
heapq.heappush(pq, (head.val, i, head))
while pq:
# Get the smallest node and attach it to the result linked list
val, i, node = heapq.heappop(pq)
p.next = node
if node.next is not None:
heapq.heappush(pq, (node.next.val, i, node.next))
# Move the p pointer forward continuously
p = p.next
return dummy.nextimport "container/heap"
// Implement heap.Interface for ListNode
type PriorityQueue []*ListNode
func (pq PriorityQueue) Len() int { return len(pq) }
func (pq PriorityQueue) Less(i, j int) bool {
return pq[i].Val < pq[j].Val
}
func (pq PriorityQueue) Swap(i, j int) {
pq[i], pq[j] = pq[j], pq[i]
}
func (pq *PriorityQueue) Push(x interface{}) {
*pq = append(*pq, x.(*ListNode))
}
func (pq *PriorityQueue) Pop() interface{} {
old := *pq
n := len(old)
x := old[n-1]
*pq = old[0 : n-1]
return x
}
func mergeKLists(lists []*ListNode) *ListNode {
if len(lists) == 0 {
return nil
}
// dummy head node
dummy := &ListNode{Val: -1}
p := dummy
// priority queue, min-heap
pq := &PriorityQueue{}
heap.Init(pq)
// add the head nodes of the k linked lists to the min-heap
for _, head := range lists {
if head != nil {
heap.Push(pq, head)
}
}
for pq.Len() > 0 {
// get the smallest node and attach it to the result linked list
node := heap.Pop(pq).(*ListNode)
p.Next = node
if node.Next != nil {
heap.Push(pq, node.Next)
}
// move the p pointer forward continuously
p = p.Next
}
return dummy.Next
}var mergeKLists = function(lists) {
if (lists.length === 0) return null;
// virtual head node
var dummy = new ListNode(-1);
var p = dummy;
// priority queue, min heap
var pq = new MinPriorityQueue({ priority: (node) => node.val });
// add the head nodes of the k linked lists to the min heap
for (var i = 0; i < lists.length; i++) {
if (lists[i] !== null) {
pq.enqueue(lists[i]);
}
}
while (!pq.isEmpty()) {
// get the smallest node and attach it to the result linked list
var node = pq.dequeue().element;
p.next = node;
if (node.next !== null) {
pq.enqueue(node.next);
}
// p pointer keeps moving forward
p = p.next;
}
return dummy.next;
}This algorithm is a common interview question. What is its time complexity?
The maximum number of elements in the priority queue pq is k, so the time complexity of a single poll or add operation is . All the linked list nodes will be added to and removed from pq, therefore, the overall time complexity of the algorithm is , where k is the number of linked lists, and N is the total number of nodes in these linked lists.
The k-th Last Node in a Singly Linked List
Finding the k-th node from the start of a singly linked list is straightforward; you can simply use a for loop to traverse the list. But how do you find the k-th node from the end?
You might say, assuming the linked list has n nodes, the k-th last node is the (n - k + 1)-th node from the start, which can also be found with a for loop, right?
Yes, but typically, algorithm problems will only provide you with a ListNode head node representing a singly linked list. You cannot directly determine the length n of the list. You need to traverse the list once to calculate the value of n, and then traverse the list again to find the (n - k + 1)-th node.
This means that this solution requires traversing the list twice to find the k-th last node.
So, can we determine the k-th last node by traversing the list only once? Yes, it can be done. If this question is asked in an interview, the interviewer is likely expecting you to provide a solution that only requires a single traversal of the list.
This solution is quite clever. Assume k = 2, and the approach is as follows:
First, let a pointer p1 point to the head node head of the list, and then move k steps:
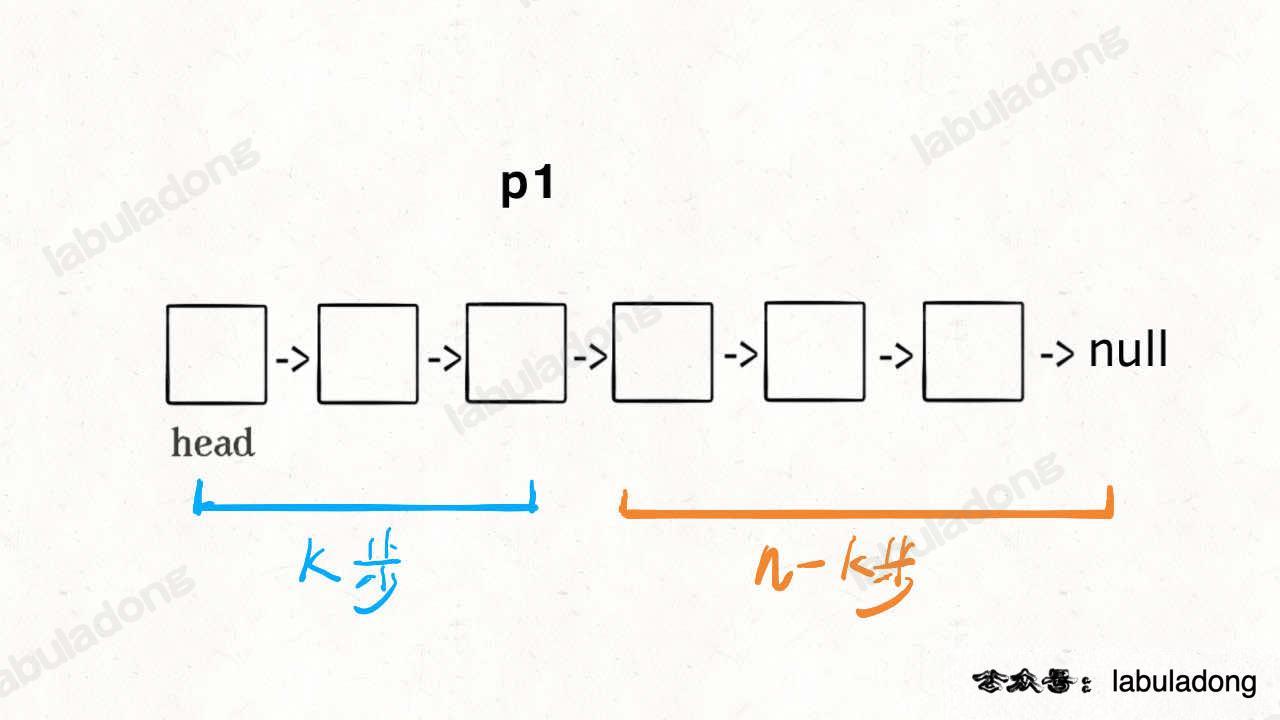
Now, p1 would need to move n - k more steps to reach the end of the list, right?
At this point, introduce another pointer p2 pointing to the head node head:
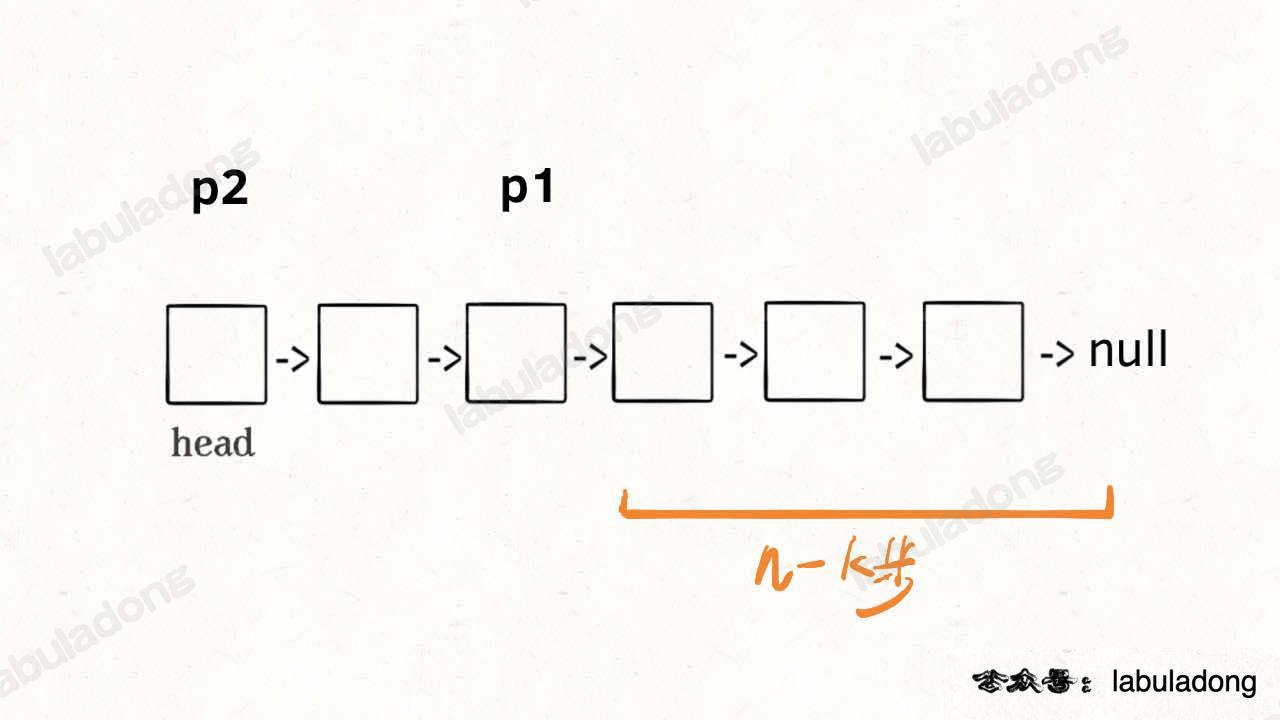
Next, it becomes clear. Move p1 and p2 forward simultaneously. When p1 reaches the end of the list, having moved n - k steps, p2 will also have moved n - k steps from head, stopping at the (n - k + 1)-th node, which is exactly the k-th last node of the list:
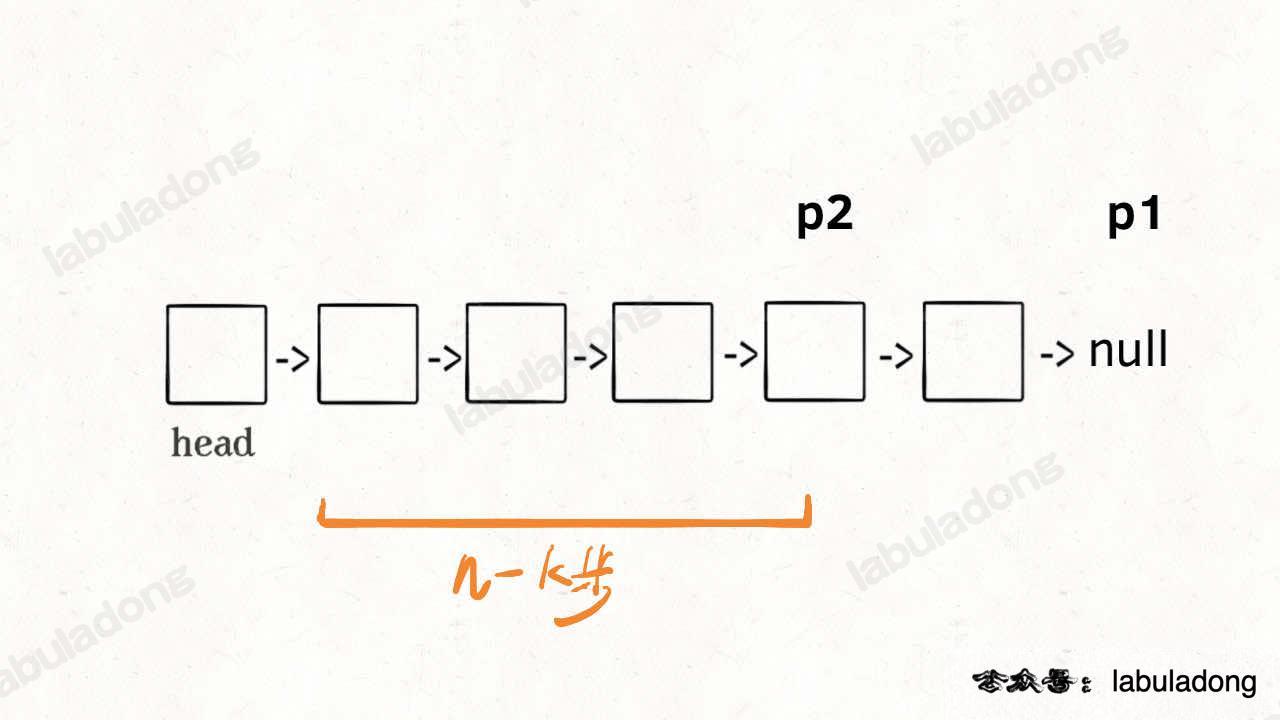
In this way, by traversing the list only once, you can obtain the k-th last node p2.
Below is the code for the above logic:
// return the k-th node from the end of the linked list
ListNode findFromEnd(ListNode head, int k) {
ListNode p1 = head;
// p1 moves k steps first
for (int i = 0; i < k; i++) {
p1 = p1.next;
}
ListNode p2 = head;
// p1 and p2 move n - k steps together
while (p1 != null) {
p2 = p2.next;
p1 = p1.next;
}
// p2 is now pointing to the (n - k + 1)-th node, which is the k-th node from the end
return p2;
}// return the k-th node from the end of the linked list
ListNode* findFromEnd(ListNode* head, int k) {
ListNode* p1 = head;
// p1 moves k steps first
for (int i = 0; i < k; i++) {
p1 = p1 -> next;
}
ListNode* p2 = head;
// p1 and p2 move n - k steps together
while (p1 != nullptr) {
p2 = p2 -> next;
p1 = p1 -> next;
}
// p2 now points to the (n - k + 1)-th node, which is the k-th node from the end
return p2;
}# return the k-th node from the end of the linked list
def findFromEnd(head: ListNode, k: int) -> ListNode:
p1 = head
# p1 goes k steps first
for i in range(k):
p1 = p1.next
p2 = head
# p1 and p2 go n - k steps together
while p1 != None:
p2 = p2.next
p1 = p1.next
# p2 now points to the (n - k + 1)-th node, which is the k-th node from the end
return p2// return the k-th node from the end of the linked list
func findFromEnd(head *ListNode, k int) *ListNode {
p1 := head
// p1 moves k steps forward
for i := 0; i < k; i++ {
p1 = p1.Next
}
p2 := head
// p1 and p2 move n - k steps together
for p1 != nil {
p1 = p1.Next
p2 = p2.Next
}
// p2 now points to the (n - k + 1)-th node, which is the k-th node from the end
return p2
}// return the k-th node from the end of the linked list
var findFromEnd = function(head, k) {
var p1 = head;
// p1 moves k steps first
for (var i = 0; i < k; i++) {
p1 = p1.next;
}
var p2 = head;
// p1 and p2 move together n - k steps
while (p1 != null) {
p2 = p2.next;
p1 = p1.next;
}
// p2 now points to the (n - k + 1)-th node, which is the k-th node from the end
return p2;
};Of course, if we use Big O notation to calculate time complexity, the time complexity for traversing a linked list once or twice is both . However, the algorithm mentioned above is more skillful.
This technique is used in many linked list-related algorithm problems, such as LeetCode Problem 19 "Remove Nth Node From End of List":
19. Remove Nth Node From End of List | LeetCode |
Given the head of a linked list, remove the nth node from the end of the list and return its head.
Example 1:
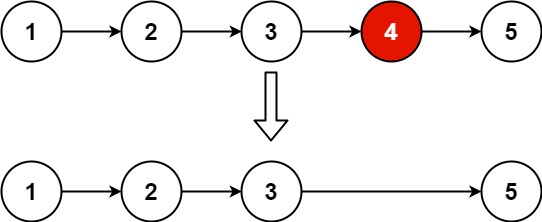
Input: head = [1,2,3,4,5], n = 2 Output: [1,2,3,5]
Example 2:
Input: head = [1], n = 1 Output: []
Example 3:
Input: head = [1,2], n = 1 Output: [1]
Constraints:
- The number of nodes in the list is
sz. 1 <= sz <= 300 <= Node.val <= 1001 <= n <= sz
Follow up: Could you do this in one pass?
Let's directly look at the solution code:
class Solution {
public ListNode removeNthFromEnd(ListNode head, int n) {
// virtual head node
ListNode dummy = new ListNode(-1);
dummy.next = head;
// to remove the nth node from the end, first find the (n + 1)th node from the end
ListNode x = findFromEnd(dummy, n + 1);
// remove the nth node from the end
x.next = x.next.next;
return dummy.next;
}
private ListNode findFromEnd(ListNode head, int k) {
// see the previous code
}
}class Solution {
public:
ListNode* removeNthFromEnd(ListNode* head, int n) {
// dummy head node
ListNode* dummy = new ListNode(-1);
dummy->next = head;
// to delete the nth node from the end, first find the (n + 1)th node from the end
ListNode* x = findFromEnd(dummy, n + 1);
// delete the nth node from the end
x->next = x->next->next;
return dummy->next;
}
private:
ListNode* findFromEnd(ListNode* head, int k) {
// code is shown above
}
};# main function
class Solution:
def removeNthFromEnd(self, head: ListNode, n: int) -> ListNode:
# dummy head node
dummy = ListNode(-1)
dummy.next = head
# to remove the nth from end, first find the (n + 1)th node from end
x = self.findFromEnd(dummy, n + 1)
# remove the nth node from end
x.next = x.next.next
return dummy.next
def findFromEnd(self, head: ListNode, k: int) -> ListNode:
# refer to the code above
passfunc removeNthFromEnd(head *ListNode, n int) *ListNode {
// virtual head node
dummy := &ListNode{Val: -1}
dummy.Next = head
// to delete the nth node from the end, first find the (n+1)th node from the end
x := findFromEnd(dummy, n+1)
// delete the nth node from the end
x.Next = x.Next.Next
return dummy.Next
}
func findFromEnd(head *ListNode, k int) *ListNode {
// code is shown above
}// main function
var removeNthFromEnd = function(head, n) {
// virtual head node
let dummy = new ListNode(-1);
dummy.next = head;
// to remove the nth node from the end, first find the (n + 1)th node from the end
let x = findFromEnd(dummy, n + 1);
// remove the nth node from the end
x.next = x.next.next;
return dummy.next;
};
var findFromEnd = function(head, k) {
// code is in the previous text
};This logic is very simple. To delete the nth node from the end, you need to get a reference to the (n + 1)th node from the end, which can be done using our implemented findFromEnd function.
However, note that we also use a dummy head node to prevent null pointer issues. For example, if the list has 5 nodes and you need to delete the 5th node from the end (i.e., the first node), the algorithm should find the 6th node from the end. But there isn't a node before the first node, which would cause an error.
With the dummy node dummy, this issue is avoided, and the deletion can be handled correctly.
Middle of a Singly Linked List
LeetCode Problem 876 "Middle of the Linked List" addresses this topic. The key problem is that we cannot directly get the length n of the singly linked list. The conventional method is to first traverse the list to calculate n, and then traverse again to get the (n / 2)th node, which is the middle node.
If you want to find the middle node in a single traversal, you need to use a bit of cleverness by employing the "slow and fast pointers" technique:
We let two pointers, slow and fast, point to the head node of the list.
Each time the slow pointer slow advances one step, the fast pointer fast advances two steps. This way, when fast reaches the end of the list, slow will be pointing to the middle of the list.
The code implementation of the above idea is as follows:
class Solution {
public ListNode middleNode(ListNode head) {
// initialize slow and fast pointers to head
ListNode slow = head, fast = head;
// stop when fast pointer reaches the end
while (fast != null && fast.next != null) {
// slow pointer moves one step, fast pointer moves two steps
slow = slow.next;
fast = fast.next.next;
}
// slow pointer points to the middle node
return slow;
}
}class Solution {
public:
ListNode* middleNode(ListNode* head) {
// initialize slow and fast pointers to head
ListNode* slow = head;
ListNode* fast = head;
// stop when fast pointer reaches the end
while (fast != nullptr && fast->next != nullptr) {
// slow pointer moves one step, fast pointer moves two steps
slow = slow->next;
fast = fast->next->next;
}
// slow pointer points to the middle node
return slow;
}
};class Solution:
def middleNode(self, head: ListNode) -> ListNode:
# initialize slow and fast pointers to head
slow, fast = head, head
# stop when the fast pointer reaches the end
while fast is not None and fast.next is not None:
# slow pointer moves one step, fast pointer moves two steps
slow = slow.next
fast = fast.next.next
# slow pointer points to the middle node
return slowfunc middleNode(head *ListNode) *ListNode {
// initialize slow and fast pointers to head
slow, fast := head, head
// stop when fast pointer reaches the end
for fast != nil && fast.Next != nil {
// slow pointer moves one step, fast pointer moves two steps
slow = slow.Next
fast = fast.Next.Next
}
// slow pointer points to the middle node
return slow
}var middleNode = function(head) {
// initialize slow and fast pointers to head
let slow = head, fast = head;
// stop when fast pointer reaches the end
while (fast !== null && fast.next !== null) {
// slow pointer moves one step, fast pointer moves two steps
slow = slow.next;
fast = fast.next.next;
}
// slow pointer points to the middle
return slow;
};It's important to note that if the length of the linked list is even, meaning there are two middle nodes, this method returns the latter one.
Additionally, with minor modifications, this code can be directly used for problems involving detecting cycles in a linked list.
Detecting Cycles in a Linked List
Determining whether a linked list contains a cycle is a classic problem, and the solution also uses the fast and slow pointer approach:
Every time the slow pointer slow moves one step forward, the fast pointer fast moves two steps forward.
If fast eventually reaches the end of the linked list normally, it means there is no cycle in the list. If fast meets slow while traversing, it indicates that fast is looping within the list, meaning there is a cycle.
You just need to slightly modify the code for finding the middle of the linked list:
class Solution {
public boolean hasCycle(ListNode head) {
// initialize slow and fast pointers to head
ListNode slow = head, fast = head;
// stop when the fast pointer reaches the end
while (fast != null && fast.next != null) {
// slow pointer moves one step, fast pointer moves two steps
slow = slow.next;
fast = fast.next.next;
// if slow and fast pointers meet, it indicates a cycle
if (slow == fast) {
return true;
}
}
// no cycle is present
return false;
}
}class Solution {
public:
bool hasCycle(ListNode *head) {
// initialize slow and fast pointers to head
ListNode *slow = head, *fast = head;
// stop when the fast pointer reaches the end
while (fast != nullptr && fast->next != nullptr) {
// slow pointer moves one step, fast pointer moves two steps
slow = slow->next;
fast = fast->next->next;
// if slow and fast pointers meet, there is a cycle
if (slow == fast) {
return true;
}
}
// no cycle
return false;
}
};class Solution:
def hasCycle(self, head: ListNode) -> bool:
# initialize slow and fast pointers to head
slow, fast = head, head
# stop when the fast pointer reaches the end
while fast is not None and fast.next is not None:
# slow pointer moves one step, fast pointer moves two steps
slow = slow.next
fast = fast.next.next
# if slow and fast pointers meet, there is a cycle
if slow == fast:
return True
# no cycle
return Falsefunc hasCycle(head *ListNode) bool {
// initialize slow and fast pointers to head
slow, fast := head, head
// stop when the fast pointer reaches the end
for fast != nil && fast.Next != nil {
// slow pointer moves one step, fast pointer moves two steps
slow = slow.Next
fast = fast.Next.Next
// if slow and fast pointers meet, a cycle is detected
if slow == fast {
return true
}
}
// no cycle detected
return false
}var hasCycle = function(head) {
// initialize slow and fast pointers to head
let slow = head, fast = head;
// stop when the fast pointer reaches the end
while (fast !== null && fast.next !== null) {
// move the slow pointer one step and the fast pointer two steps
slow = slow.next;
fast = fast.next.next;
// if slow and fast pointers meet, it indicates a cycle
if (slow === fast) {
return true;
}
}
// no cycle detected
return false;
};Certainly, there is an advanced version of this problem, which is LeetCode Problem 142 "Linked List Cycle II": How do you find the starting point of a cycle in a linked list?
To avoid confusion, let's consider an example. The starting point of the cycle is node 2 in the following diagram:
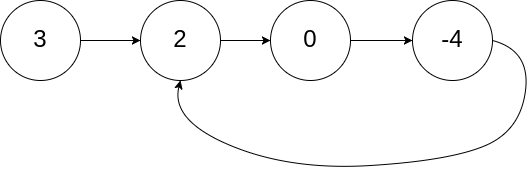
Let's first take a look at the code for finding the starting point of the cycle:
class Solution {
public ListNode detectCycle(ListNode head) {
ListNode fast, slow;
fast = slow = head;
while (fast != null && fast.next != null) {
fast = fast.next.next;
slow = slow.next;
if (fast == slow) break;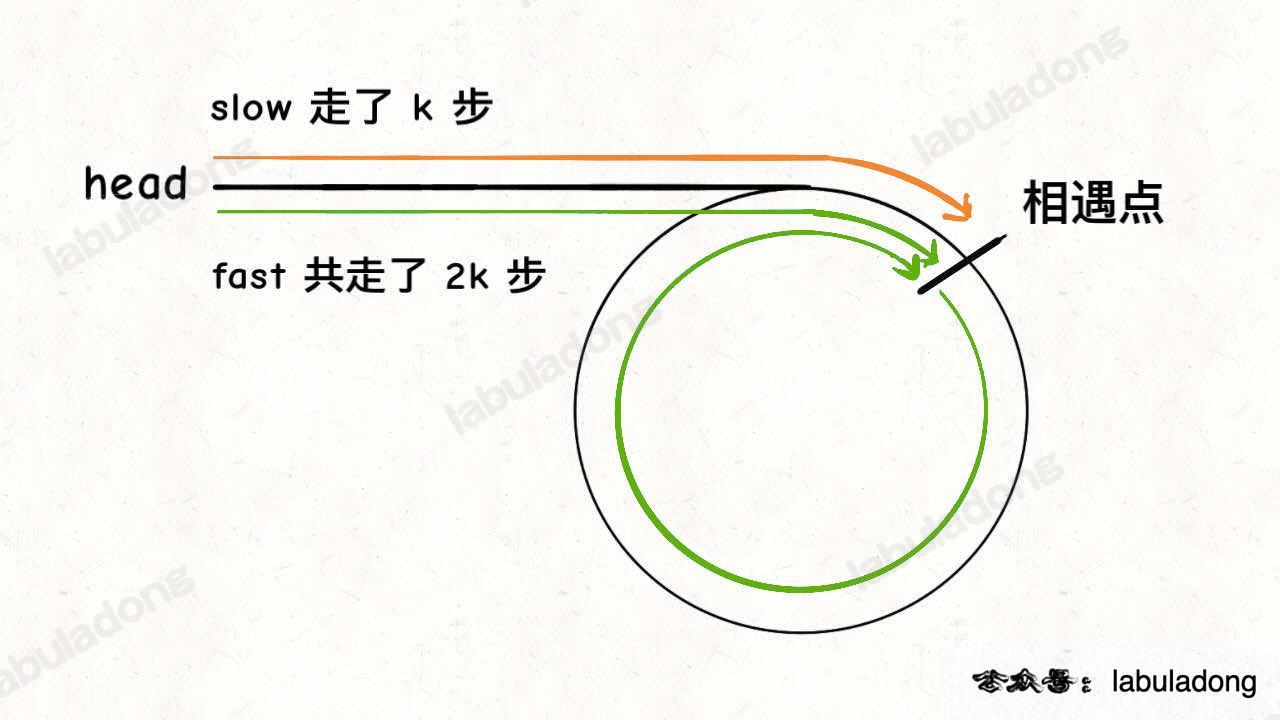
}
// the above code is similar to the hasCycle function
if (fast == null || fast.next == null) {
// fast encountering a null pointer means there is no cycle
return null;
}
// reassign to the head node
slow = head;
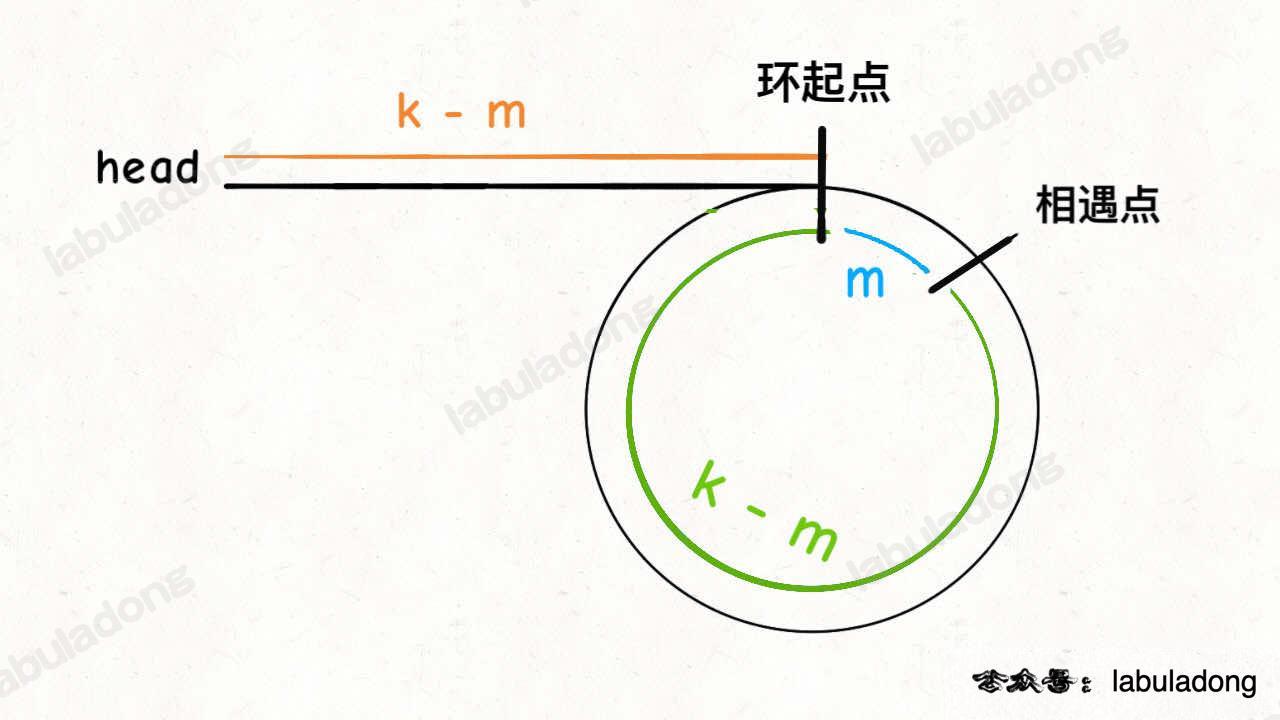// move fast and slow pointers at the same pace, the intersection point is the cycle's entry point
while (slow != fast) {
fast = fast.next;
slow = slow.next;
}
return slow;
}
}class Solution {
public:
ListNode* detectCycle(ListNode* head) {
ListNode* fast = head;
ListNode* slow = head;
while (fast != nullptr && fast->next != nullptr) {
fast = fast->next->next;
slow = slow->next;
if (fast == slow) break;
}
// The above code is similar to the hasCycle function
if (fast == nullptr || fast->next == nullptr) {
// fast encountering a null pointer means there is no cycle
return nullptr;
}
// re-point to the head node
slow = head;
// move fast and slow pointers forward at the same pace, the meeting point is the cycle's starting point
while (slow != fast) {
fast = fast->next;
slow = slow->next;
}
return slow;
}
};class Solution:
def detectCycle(self, head: ListNode) -> ListNode:
fast, slow = head, head
while fast and fast.next:
fast = fast.next.next
slow = slow.next
if fast == slow:
break
if not fast or not fast.next:
return None
slow = head
while slow != fast:
fast = fast.next
slow = slow.next
return slowfunc detectCycle(head *ListNode) *ListNode {
var fast, slow *ListNode
fast, slow = head, head
for fast != nil && fast.Next != nil {
fast = fast.Next.Next
slow = slow.Next
if fast == slow {
break
}
}
if fast == nil || fast.Next == nil {
return nil
}
slow = head
for slow != fast {
slow = slow.Next
fast = fast.Next
}
return slow
}var detectCycle = function(head) {
var fast, slow;
fast = slow = head;
while (fast != null && fast.next != null) {
fast = fast.next.next;
slow = slow.next;
if (fast == slow) break;
}
// The above code is similar to the hasCycle function
if (fast == null || fast.next == null) {
// fast encountering a null pointer means there is no cycle
return null;
}
// Re-point to the head node
slow = head;
// Fast and slow pointers move forward synchronously, and the intersection point is the start of the cycle
while (slow != fast) {
fast = fast.next;
slow = slow.next;
}
return slow;
};It can be observed that when the fast and slow pointers meet, if you set one of the pointers to the head node and let them move forward at the same speed, the node where they meet again is the starting point of the cycle.
Why does this work? Let's briefly explain the principle behind it.
Assume that when the fast and slow pointers meet, the slow pointer slow has taken k steps, then the fast pointer fast must have taken 2k steps:
The fast pointer must have taken k more steps than slow. These extra k steps are essentially the fast pointer circling within the loop, so the value of k is a "multiple of the loop's length."
Assume the distance from the meeting point to the start of the loop is m. Then, according to the diagram with the slow pointer, the distance from the loop's start to the head node head is k - m. This means if we move forward k - m steps from head, we will reach the loop's start.
Interestingly, if we move forward k - m steps from the meeting point, we also reach the loop's start. Based on the diagram with the fast pointer, starting from the meeting point and moving k steps brings us back to the meeting point, so moving k - m steps will definitely bring us to the loop's start:
Therefore, if we redirect one of the fast or slow pointers to head, and let both pointers move at the same speed, they will meet at the loop's start after k - m steps.
Do Two Linked Lists Intersect?
This is an interesting problem, also known as LeetCode Problem 160 "Intersection of Two Linked Lists," with the function signature as follows:
ListNode getIntersectionNode(ListNode headA, ListNode headB);ListNode* getIntersectionNode(ListNode* headA, ListNode* headB);def getIntersectionNode(headA: ListNode, headB: ListNode) -> ListNode:func getIntersectionNode(headA *ListNode, headB *ListNode) *ListNodevar getIntersectionNode = function(headA, headB)You are given the head nodes headA and headB of two linked lists, which may intersect.
If they intersect, your algorithm should return the intersecting node; if not, it should return null.
For instance, in the example provided, if the input linked lists are as shown in the image below:
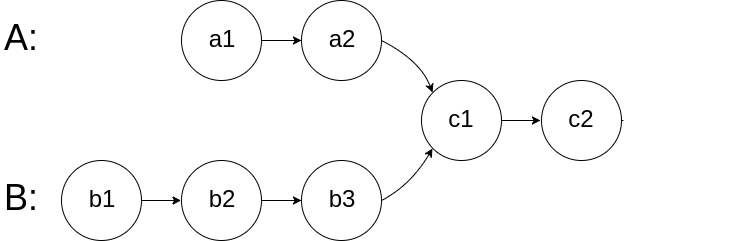
Then your algorithm should return the node c1.
A straightforward approach might be to use a HashSet to record all the nodes of one linked list and then compare with the other linked list, but this requires extra space.
How could you solve this using only two pointers, without additional space?
The challenge lies in the fact that the lengths of the two linked lists may differ, so their nodes do not align:
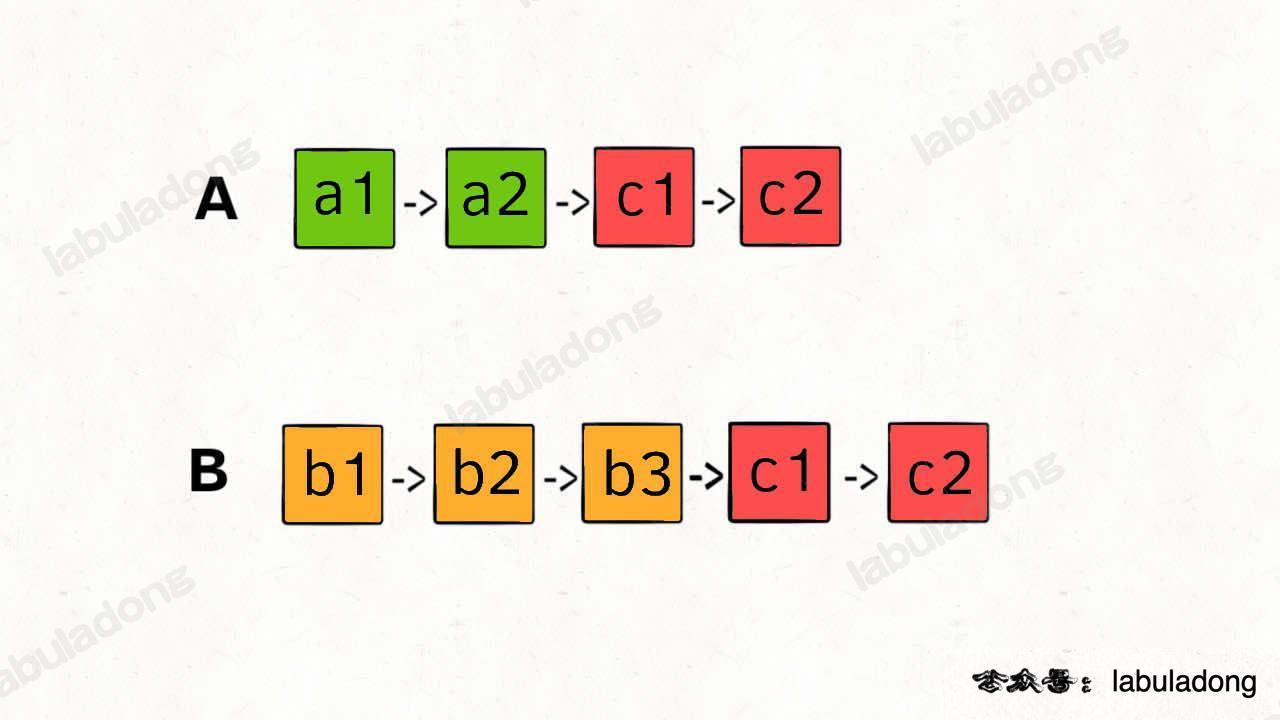
If you move two pointers, p1 and p2, along the two linked lists, they cannot simultaneously reach the common node, and thus, cannot find the intersecting node c1.
The key to solving this problem is to make p1 and p2 reach the intersecting node c1 simultaneously through some method.
So, we can let p1 traverse through list A and then start traversing list B, while p2 traverses through list B and then starts traversing list A. This approach effectively "logically" connects the two linked lists.
By doing this, p1 and p2 can enter the common section simultaneously, reaching the intersecting node c1:
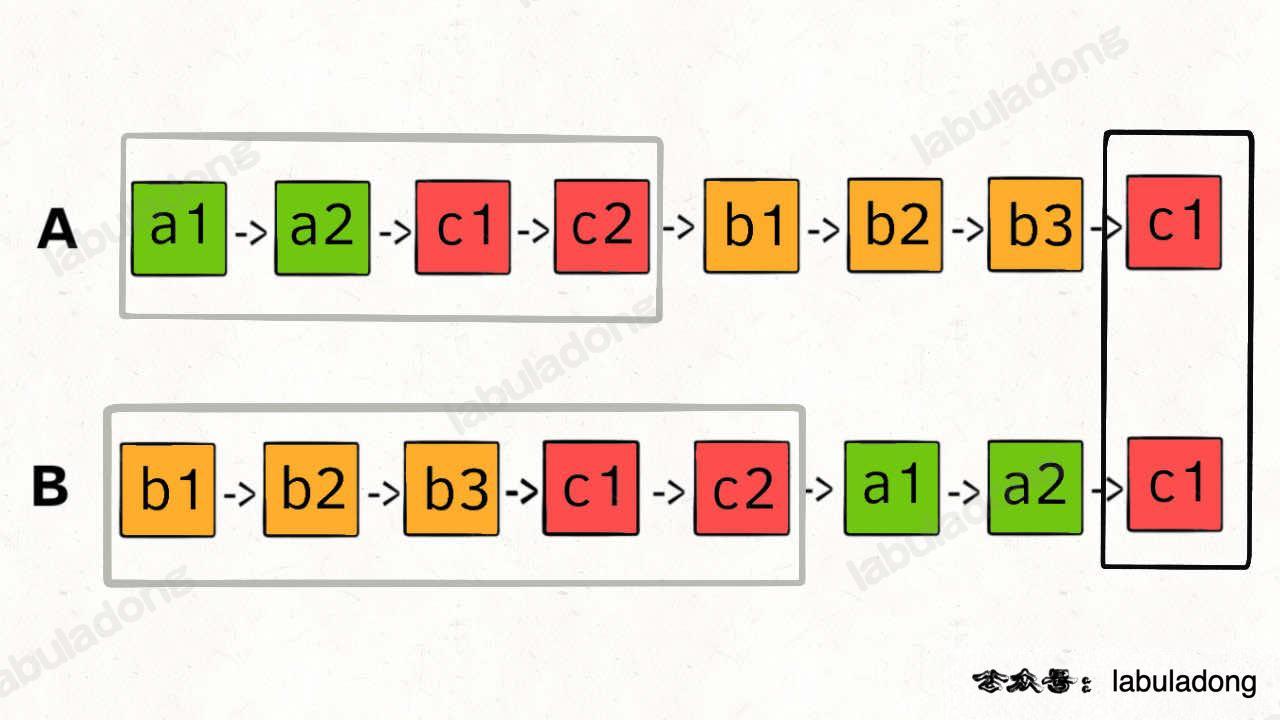
You might wonder, if the two linked lists do not intersect, will it correctly return null?
This logic can indeed handle such a situation, as it treats the c1 node as a null pointer, correctly returning null.
Following this idea, the code can be written as follows:
class Solution {
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
// p1 points to the head node of list A, p2 points to the head node of list B
ListNode p1 = headA, p2 = headB;
while (p1 != p2) {
// p1 takes a step, if it reaches the end of list A, switch to list B
if (p1 == null) {
p1 = headB;
} else {
p1 = p1.next;
}
// p2 takes a step, if it reaches the end of list B, switch to list A
if (p2 == null) {
p2 = headA;
} else{
p2 = p2.next;
}
}
return p1;
}
}class Solution {
public:
ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
// p1 points to the head of list A, p2 points to the head of list B
ListNode *p1 = headA, *p2 = headB;
while (p1 != p2) {
// p1 moves one step, if it reaches the end of list A, switch to list B
if (p1 == nullptr) {
p1 = headB;
} else {
p1 = p1->next;
}
// p2 moves one step, if it reaches the end of list B, switch to list A
if (p2 == nullptr) {
p2 = headA;
} else {
p2 = p2->next;
}
}
return p1;
}
};class Solution:
def getIntersectionNode(self, headA: ListNode, headB: ListNode) -> ListNode:
# p1 points to the head node of list A, p2 points to the head node of list B
p1, p2 = headA, headB
while p1 != p2:
# p1 moves one step, if it reaches the end of list A, switch to list B
p1 = p1.next if p1 else headB
# p2 moves one step, if it reaches the end of list B, switch to list A
p2 = p2.next if p2 else headA
return p1func getIntersectionNode(headA, headB *ListNode) *ListNode {
// p1 points to the head node of list A, p2 points to the head node of list B
p1 := headA
p2 := headB
for p1 != p2 {
// p1 takes a step, if it reaches the end of list A, switch to list B
if p1 == nil {
p1 = headB
} else {
p1 = p1.Next
}
// p2 takes a step, if it reaches the end of list B, switch to list A
if p2 == nil {
p2 = headA
} else {
p2 = p2.Next
}
}
return p1
}var getIntersectionNode = function(headA, headB) {
// p1 points to the head node of list A, p2 points to the head node of list B
let p1 = headA, p2 = headB;
while (p1 !== p2) {
// p1 takes one step, if it reaches the end of list A, switch to list B
if (p1 === null) {
p1 = headB;
} else {
p1 = p1.next;
}
// p2 takes one step, if it reaches the end of list B, switch to list A
if (p2 === null) {
p2 = headA;
} else {
p2 = p2.next;
}
}
return p1;
};Thus, this problem is solved with a space complexity of and a time complexity of .
These are all the techniques for singly linked lists. I hope they inspire you.
Update on 2022/1/24:
Several excellent readers have proposed alternative approaches to the last problem, "Finding the Intersection of Two Linked Lists," which are also included here.
Initially, a reader mentioned that if you connect the two linked lists end to end, the problem of "finding the intersection of two linked lists" transforms into the previously discussed problem of "finding the start of a loop":
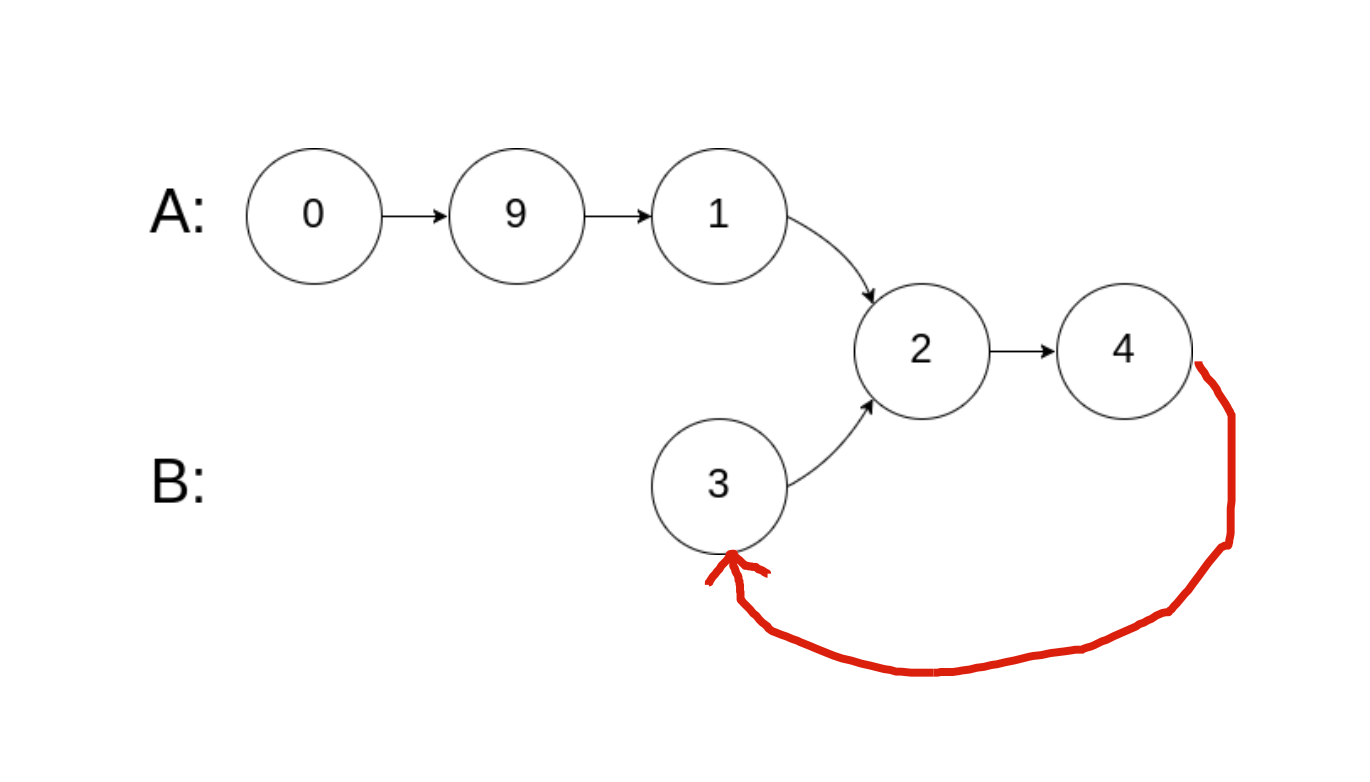
Honestly, I did not think of this approach. It's a clever transformation! However, it's important to note that the problem states you should not alter the original structure of the linked lists, so after transforming the input linked lists into a circular linked list to solve the problem, remember to revert them back; otherwise, you won't pass.
Additionally, another reader suggested that since the core of "finding the intersection of two linked lists" lies in having pointers p1 and p2 simultaneously reach the intersecting node c1, you can achieve this by pre-calculating the lengths of the two linked lists. The specific code is as follows:
class Solution {
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
int lenA = 0, lenB = 0;
// calculate the lengths of the two linked lists
for (ListNode p1 = headA; p1 != null; p1 = p1.next) {
lenA++;
}
for (ListNode p2 = headB; p2 != null; p2 = p2.next) {
lenB++;
}
// make p1 and p2 the same distance from the end
ListNode p1 = headA, p2 = headB;
if (lenA > lenB) {
for (int i = 0; i < lenA - lenB; i++) {
p1 = p1.next;
}
} else {
for (int i = 0; i < lenB - lenA; i++) {
p2 = p2.next;
}
}
// check if the two pointers become the same, when p1 == p2, there are two scenarios:
// 1. either the two linked lists do not intersect, they both move to the end null pointer
// 2. or the two linked lists intersect, they reach the intersection point of the two linked lists
while (p1 != p2) {
p1 = p1.next;
p2 = p2.next;
}
return p1;
}
}class Solution {
public:
ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
int lenA = 0, lenB = 0;
// calculate the lengths of the two linked lists
for (ListNode* p1 = headA; p1 != nullptr; p1 = p1->next) {
lenA++;
}
for (ListNode* p2 = headB; p2 != nullptr; p2 = p2->next) {
lenB++;
}
// make the distance to the end equal for p1 and p2
ListNode* p1 = headA;
ListNode* p2 = headB;
if (lenA > lenB) {
for (int i = 0; i < lenA - lenB; i++) {
p1 = p1->next;
}
} else {
for (int i = 0; i < lenB - lenA; i++) {
p2 = p2->next;
}
}
// check if the two pointers are the same, there are two cases when p1 == p2:
// 1. either the two linked lists do not intersect, and they both reach the end null pointer
// 2. or the two linked lists intersect, and they reach the intersection point of the two linked lists
while (p1 != p2) {
p1 = p1->next;
p2 = p2->next;
}
return p1;
}
};class Solution:
def getIntersectionNode(self, headA: ListNode, headB: ListNode) -> ListNode:
lenA, lenB = 0, 0
# calculate the length of both linked lists
p1, p2 = headA, headB
while p1:
lenA += 1
p1 = p1.next
while p2:
lenB += 1
p2 = p2.next
# make p1 and p2 reach the same distance from the end
p1, p2 = headA, headB
if lenA > lenB:
for _ in range(lenA - lenB):
p1 = p1.next
else:
for _ in range(lenB - lenA):
p2 = p2.next
# check if the two pointers are the same, there are two cases when p1 == p2:
# 1. either the two linked lists do not intersect and both reach the end null pointer
# 2. or the two linked lists intersect and they reach the intersection point
while p1 != p2:
p1 = p1.next
p2 = p2.next
return p1func getIntersectionNode(headA, headB *ListNode) *ListNode {
lenA, lenB := 0, 0
// calculate the lengths of the two linked lists
for p1 := headA; p1 != nil; p1 = p1.Next {
lenA++
}
for p2 := headB; p2 != nil; p2 = p2.Next {
lenB++
}
// make p1 and p2 reach the same distance from the end
p1, p2 := headA, headB
if lenA > lenB {
for i := 0; i < lenA - lenB; i++ {
p1 = p1.Next
}
} else {
for i := 0; i < lenB - lenA; i++ {
p2 = p2.Next
}
}
// see if the two pointers will be the same, when p1 == p2 there are two cases:
// 1. either the two linked lists do not intersect, and they simultaneously reach the null pointer at the end
// 2. or the two linked lists intersect, and they reach the intersection point of the two linked lists
for p1 != p2 {
p1 = p1.Next
p2 = p2.Next
}
return p1
}var getIntersectionNode = function(headA, headB) {
let lenA = 0, lenB = 0;
// calculate the lengths of the two linked lists
for (let p1 = headA; p1 != null; p1 = p1.next) {
lenA++;
}
for (let p2 = headB; p2 != null; p2 = p2.next) {
lenB++;
}
// make p1 and p2 have the same distance to the end
let p1 = headA, p2 = headB;
if (lenA > lenB) {
for (let i = 0; i < lenA - lenB; i++) {
p1 = p1.next;
}
} else {
for (let i = 0; i < lenB - lenA; i++) {
p2 = p2.next;
}
}
// check if the two pointers become the same, there are two cases when p1 == p2:
// 1. either the two linked lists do not intersect, and they both reach the null pointer at the end
// 2. or the two linked lists intersect, and they reach the intersection point
while (p1 != p2) {
p1 = p1.next;
p2 = p2.next;
}
return p1;
};Although the code might be a bit longer, the time complexity remains , and it is somewhat easier to understand.
In conclusion, my solution is not necessarily the most optimal or correct one. I encourage everyone to raise their own questions and thoughts in the comments section. I am also pleased to discuss more problem-solving approaches with you all.
This concludes the discussion on the two-pointer techniques related to linked lists. For more extended applications of these techniques, see More Classic Linked List Two-Pointer Problems.
Related Problems
You can install my Chrome extension then open the link.