Binary Tree Recursive/Level Traversal

labuladongOriginalAbout 5650 words

Prerequisite Knowledge

Before reading this article, you should first learn:

Recursive/Level Order Traversal of Binary Trees

Having understood the basic concepts and special types of binary trees, this article will explain how to traverse and access the nodes of a binary tree.

Recursive Traversal (DFS)

The framework for traversing a binary tree:

java 🟢

// basic binary tree node
class TreeNode {
    int val;
    TreeNode left, right;
}

// traversal framework for binary tree
void traverse(TreeNode root) {
    if (root == null) {
        return;
    }
    traverse(root.left);
    traverse(root.right);
}

cpp 🤖

// basic binary tree node
class TreeNode {
public:
    int val;
    TreeNode* left;
    TreeNode* right;

    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};

// binary tree traversal framework
void traverse(TreeNode* root) {
    if (root == nullptr) {
        return;
    }
    traverse(root->left);
    traverse(root->right);
}

python 🤖

# basic binary tree node
class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

# traversal framework for binary tree
def traverse(root: TreeNode):
    if root is None:
        return
    traverse(root.left)
    traverse(root.right)

go 🤖

// basic binary tree node
type TreeNode struct {
    Val   int
    Left  *TreeNode
    Right *TreeNode
}

// binary tree traversal framework
func traverse(root *TreeNode) {
    if root == nil {
        return
    }
    traverse(root.Left)
    traverse(root.Right)
}

javascript 🤖

// basic binary tree node
class TreeNode {
    constructor(val) {
        this.val = val;
        this.left = null;
        this.right = null;
    }
}

// binary tree traversal framework
var traverse = function(root) {
    if (root === null) {
        return;
    }
    traverse(root.left);
    traverse(root.right);
}

Why can this short and concise code traverse a binary tree? And in what order does it traverse the tree?

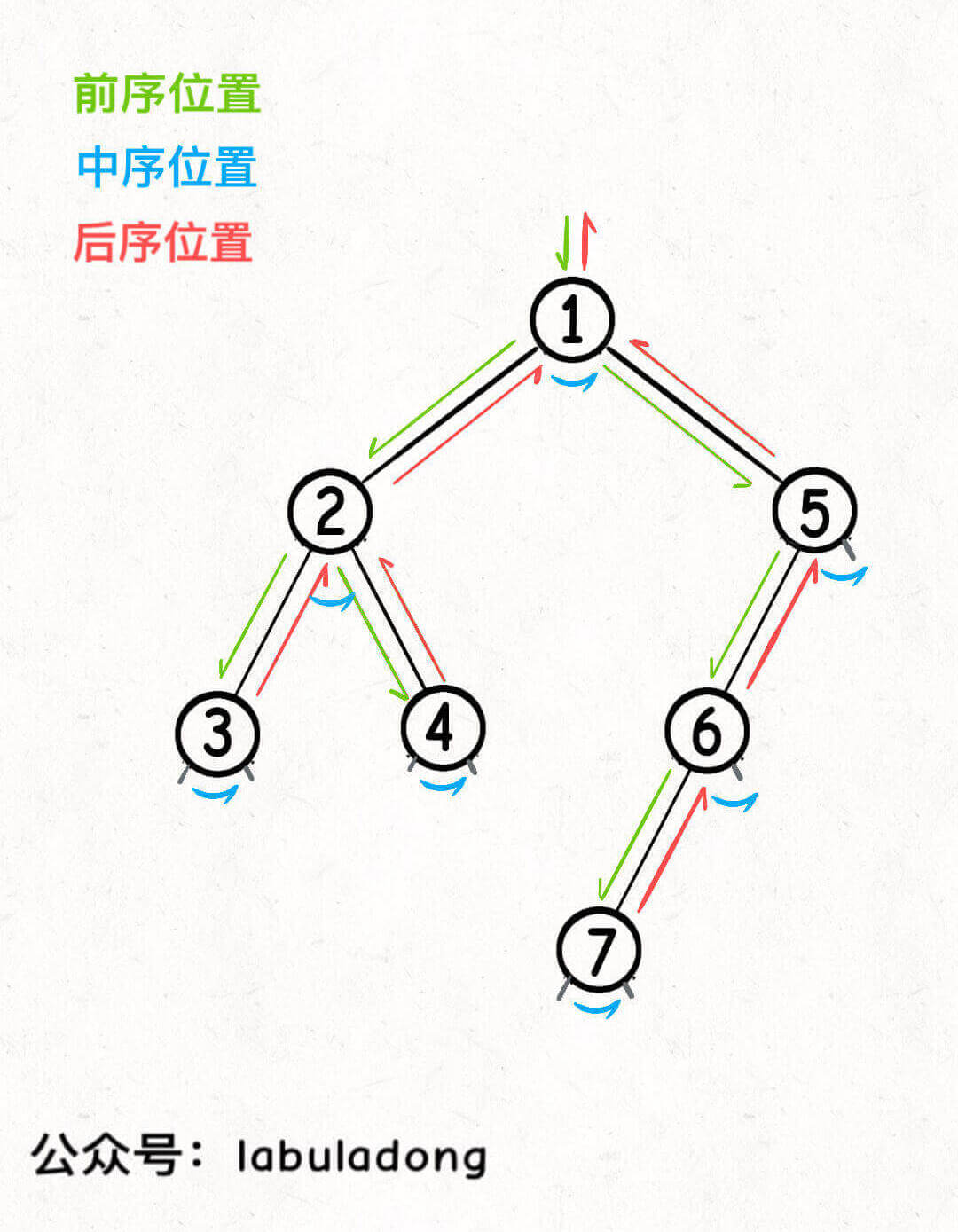
For a recursive traversal function like traverse, you can think of it as a pointer that moves around the binary tree structure. Below, I'll use a visualization to show you how this function traverses the binary tree intuitively.

Open this visualization panel, and the position of the root pointer on the right is the node currently being visited, which is the current position of the traverse function. The orange-yellow part shows the stack of the traverse function. You can click the play button at the top left to observe the changes in the position of the root pointer:

The traversal order of the traverse function is to keep moving to the left child node until it encounters a null pointer and can't go further, then it tries to move one step to the right child node; then it tries moving left again, repeating this cycle. If both left and right subtrees are done, it returns to the parent node. You can see this from the code: it first recursively calls root.left, then root.right.

This recursive traversal node order is fixed, and you must remember this order. Otherwise, you won't manage the binary tree structure effectively.

Readers with some data structure background might ask: Wait a minute, everyone who has taken a data structures course knows there are pre-order, in-order, and post-order traversals, resulting in three different orders. Why do you say the recursive traversal order is fixed?

That's a great question, let me explain.

Important

The order of recursive traversal, that is, the order in which the traverse function visits nodes, is indeed fixed. As shown in the visualization panel, the order in which the root pointer moves in the tree is fixed.

However, the effect can vary depending on where you write the code within the traverse function. The reason pre-order, in-order, and post-order traversals differ is because the code is written in different places, resulting in different effects.

For example, when you first enter a node, you know nothing about its child nodes, but when you leave a node, you have visited all its child nodes. Writing code in these two situations can lead to different outcomes.

What you refer to as pre-order, in-order, and post-order traversals is actually about writing code at different points in this binary tree traversal framework:

java 🟢

// Binary tree traversal framework
void traverse(TreeNode root) {
    if (root == null) {
        return;
    }
    // pre-order position
    traverse(root.left);
    // in-order position
    traverse(root.right);
    // post-order position
}

cpp 🤖

// binary tree traversal framework
void traverse(TreeNode* root) {
    if (root == nullptr) {
        return;
    }
    // pre-order position
    traverse(root->left);
    // in-order position
    traverse(root->right);
    // post-order position
}

python 🤖

# Binary tree traversal framework
def traverse(root):
    if root is None:
        return
    # Pre-order position
    traverse(root.left)
    # In-order position
    traverse(root.right)
    # Post-order position

go 🤖

// Binary tree traversal framework
func traverse(root *TreeNode) {
    if root == nil {
        return
    }
    // Preorder position
    traverse(root.Left)
    // Inorder position
    traverse(root.Right)
    // Postorder position
}

javascript 🤖

// binary tree traversal framework
var traverse = function(root) {
    if (root === null) {
        return;
    }
    // pre-order position
    traverse(root.left);
    // in-order position
    traverse(root.right);
    // post-order position
};

The code at the preorder position executes when entering a node; the code at the inorder position executes after traversing the left subtree and before traversing the right subtree; the code at the postorder position executes after both subtrees have been traversed:

You can open this visualization panel and try the following actions:

Continuously click the line preorderResult.push and observe the order in which the root pointer moves through the tree and the elements in preorderResult. This demonstrates the preorder traversal order.
Reset the visualization panel, continuously click the line inorderResult.push, and observe the movement of the root pointer and the elements in inorderResult. This demonstrates the inorder traversal order.
Reset the visualization panel, continuously click the line postorderResult.push, and observe the movement of the root pointer and the elements in postorderResult. This demonstrates the postorder traversal order.

The positions for preorder, inorder, and postorder in a binary tree are crucial. I will explore the differences and connections between them, and how they can be applied in backtracking and dynamic programming algorithms, in Binary Tree Algorithm Thoughts (Guideline) and exercises. This will not be elaborated here.

Some readers might ask, why does the traverse function first recursively traverse root.left and then root.right? Can it be reversed?

Of course, it can be reversed. However, the conventional preorder, inorder, and postorder traversals assume left before right, which is a customary practice. If you choose to traverse right before left, your understanding of these traversals will differ from the norm, which could complicate communication. Therefore, unless there's a specific requirement, it's best to write code following the left-to-right order.

The Inorder Traversal of a BST is Ordered

It's important to emphasize that the inorder traversal result of a Binary Search Tree (BST) is ordered, which is a significant property of BSTs.

You can view this visualization panel and click the line res.push(root.val); to see the order in which nodes are accessed during an inorder traversal:

In the subsequent BST-related exercise set, some problems will utilize this property.

Level Order Traversal (BFS)

The above recursive traversal relies on the function stack to recursively traverse the binary tree. If you consider the recursive function traverse as a pointer, then the order in which this pointer moves through the binary tree roughly starts from the far left and goes column by column to the far right.

You can use the visualization panel and click on the line of code if (root == null) to see the order in which the root variable moves through the tree. This will give you a clear view of the order in which the traverse function visits the nodes:

Level order traversal of a binary tree, as the name suggests, means traversing the tree level by level. This traversal method requires the use of a queue, and depending on different needs, there are mainly three different ways to write it. Below are the examples one by one.

Method One

This is the simplest method, and the code is as follows:

java 🟢

void levelOrderTraverse(TreeNode root) {
    if (root == null) {
        return;
    }
    Queue<TreeNode> q = new LinkedList<>();
    q.offer(root);
    while (!q.isEmpty()) {
        TreeNode cur = q.poll();
        // visit the cur node
        System.out.println(cur.val);

        // add the left and right children of cur to the queue
        if (cur.left != null) {
            q.offer(cur.left);
        }
        if (cur.right != null) {
            q.offer(cur.right);
        }
    }
}

cpp 🤖

void levelOrderTraverse(TreeNode* root) {
    if (root == nullptr) {
        return;
    }
    std::queue<TreeNode*> q;
    q.push(root);
    while (!q.empty()) {
        TreeNode* cur = q.front();
        q.pop();
        // visit the cur node
        std::cout << cur->val << std::endl;
        
        // add the left and right children of cur to the queue
        if (cur->left != nullptr) {
            q.push(cur->left);
        }
        if (cur->right != nullptr) {
            q.push(cur->right);
        }
    }
}

python 🤖

from collections import deque

def levelOrderTraverse(root):
    if root is None:
        return
    q = deque()
    q.append(root)
    while q:
        cur = q.popleft()
        # visit cur node
        print(cur.val)

        # add cur's left and right children to the queue
        if cur.left is not None:
            q.append(cur.left)
        if cur.right is not None:
            q.append(cur.right)

go 🤖

func levelOrderTraverse(root *TreeNode) {
    if root == nil {
        return
    }
    q := []*TreeNode{}
    q = append(q, root)
    for len(q) > 0 {
        cur := q[0]
        q = q[1:]
        // visit cur node
        fmt.Println(cur.Val)
        
        // add cur's left and right children to the queue
        if cur.Left != nil {
            q = append(q, cur.Left)
        }
        if cur.Right != nil {
            q = append(q, cur.Right)
        }
    }
}

javascript 🤖

var levelOrderTraverse = function(root) {
    if (root === null) {
        return;
    }
    var q = [];
    q.push(root);
    while (q.length !== 0) {
        var cur = q.shift();
        // visit cur node
        console.log(cur.val);

        // add cur's left and right children to the queue
        if (cur.left !== null) {
            q.push(cur.left);
        }
        if (cur.right !== null) {
            q.push(cur.right);
        }
    }
}

You can open this visualization panel and click on the line of code console.log(cur.val);. By observing the order in which the cur variable moves through the tree, you can see that level order traversal checks the binary tree nodes level by level, from left to right:

Advantages and Disadvantages of This Approach

The biggest advantage of this approach is its simplicity. Each time, you take the front element from the queue, then add its left and right child nodes to the queue, and that's it.

However, the drawback of this approach is that it doesn't allow you to know which level the current node is on. Knowing the level of a node is a common requirement, for example, if you need to collect nodes from each level or calculate the minimum depth of a binary tree.

So, although this method is simple, it's not used often. The approach introduced below is more commonly used.

Approach Two

With a slight modification to the above solution, we get the following approach:

java 🟢

void levelOrderTraverse(TreeNode root) {
    if (root == null) {
        return;
    }
    Queue<TreeNode> q = new LinkedList<>();
    q.offer(root);
    // record the current level being traversed (root node is considered as level 1)
    int depth = 1;

    while (!q.isEmpty()) {
        int sz = q.size();
        for (int i = 0; i < sz; i++) {
            TreeNode cur = q.poll();
            // visit the cur node and know its level
            System.out.println("depth = " + depth + ", val = " + cur.val);

            // add the left and right children of cur to the queue
            if (cur.left != null) {
                q.offer(cur.left);
            }
            if (cur.right != null) {
                q.offer(cur.right);
            }
        }
        depth++;
    }
}

cpp 🤖

void levelOrderTraverse(TreeNode* root) {
    if (root == nullptr) {
        return;
    }
    queue<TreeNode*> q;
    q.push(root);
    // record the current level being traversed (the root node is considered as level 1)
    int depth = 1;

    while (!q.empty()) {
        int sz = q.size();
        for (int i = 0; i < sz; i++) {
            TreeNode* cur = q.front();
            q.pop();
            // visit the cur node, knowing its level
            cout << "depth = " << depth << ", val = " << cur->val << endl;

            // add the left and right children of cur to the queue
            if (cur->left != nullptr) {
                q.push(cur->left);
            }
            if (cur->right != nullptr) {
                q.push(cur->right);
            }
        }
        depth++;
    }
}

python 🤖

from collections import deque

def levelOrderTraverse(root):
    if root is None:
        return
    q = deque()
    q.append(root)
    # record the current depth being traversed (root node is considered as level 1)
    depth = 1

    while q:
        sz = len(q)
        for i in range(sz):
            cur = q.popleft()
            # visit cur node and know its depth
            print(f"depth = {depth}, val = {cur.val}")

            # add cur's left and right children to the queue
            if cur.left is not None:
                q.append(cur.left)
            if cur.right is not None:
                q.append(cur.right)
        depth += 1

go 🤖

func levelOrderTraverse(root *TreeNode) {
    if root == nil {
        return
    }
    q := []*TreeNode{root}
    // record the current depth being traversed (root node is considered as level 1)
    depth := 1

    for len(q) > 0 {
        // get the current queue length
        sz := len(q)
        for i := 0; i < sz; i++ {
            // dequeue the front of the queue
            cur := q[0]
            q = q[1:]
            // visit the cur node and know its depth
            fmt.Printf("depth = %d, val = %d\n", depth, cur.Val)

            // add cur's left and right children to the queue
            if cur.Left != nil {
                q = append(q, cur.Left)
            }
            if cur.Right != nil {
                q = append(q, cur.Right)
            }
        }
        depth++
    }
}

javascript 🤖

var levelOrderTraverse = function(root) {
    if (root === null) {
        return;
    }
    var q = [];
    q.push(root);
    // record the current depth (root node is considered as level 1)
    var depth = 1;

    while (q.length !== 0) {
        var sz = q.length;
        for (var i = 0; i < sz; i++) {
            var cur = q.shift();
            // visit the cur node and know its depth
            console.log("depth = " + depth + ", val = " + cur.val);

            // add the left and right children of cur to the queue
            if (cur.left !== null) {
                q.push(cur.left);
            }
            if (cur.right !== null) {
                q.push(cur.right);
            }
        }
        depth++;
    }
};

Note

Pay attention to the inner for loop in the code:

int sz = q.size();
for (int i = 0; i < sz; i++) {
    ...
}

The variable i keeps track of the position of the node cur in the current level. In most algorithm problems, you won't need this variable, so you can use the following approach instead:

int sz = q.size();
while (sz-- > 0) {
    ...
}

This is a detail matter, so feel free to choose based on your preference.

But make sure to save the queue length sz before starting the loop, because the queue length changes during the loop, and you can't use q.size() directly as the loop condition.

You can open this visualization panel and click on the console.log line of code to see how the cur variable moves through the tree. You'll observe that it still traverses the binary tree level by level, from left to right, but this time it also outputs the level of each node:

This approach allows you to record the level of each node, which can solve problems like finding the minimum depth of a binary tree. It's our most common way of performing level order traversal.

Approach Three

If approach two is the most common, why is there an approach three? It's to lay the groundwork for more advanced topics.

Right now, we're just discussing binary tree level order traversal, but this can extend to N-ary tree level order traversal, graph BFS traversal, and the classic BFS brute force algorithm framework. So, we need to expand a bit here.

Revisiting approach two, we increment depth by 1 each time we go down a level. You can think of each branch having a weight of 1. The depth of each node in a binary tree is actually the total weight of the path from the root to that node, and all nodes on the same level have the same path weight sum.

Now, imagine if the weight of each branch could be any value, and you need to perform a level order traversal of the entire tree, printing the path weight sum for each node. How would you do it?

In this case, nodes on the same level might not have the same path weight sum, and maintaining just one depth variable, as in approach two, wouldn't suffice.

Approach three addresses this by adding a State class to approach one, allowing each node to maintain its own path weight sum. Here's the code:

java 🟢

class State {
    TreeNode node;
    int depth;

    State(TreeNode node, int depth) {
        this.node = node;
        this.depth = depth;
    }
}

void levelOrderTraverse(TreeNode root) {
    if (root == null) {
        return;
    }
    Queue<State> q = new LinkedList<>();
    // the path weight sum of the root node is 1
    q.offer(new State(root, 1));

    while (!q.isEmpty()) {
        State cur = q.poll();
        // visit the cur node, while knowing its path weight sum
        System.out.println("depth = " + cur.depth + ", val = " + cur.node.val);

        // add the left and right child nodes of cur to the queue
        if (cur.node.left != null) {
            q.offer(new State(cur.node.left, cur.depth + 1));
        }
        if (cur.node.right != null) {
            q.offer(new State(cur.node.right, cur.depth + 1));
        }
    }
}

cpp 🤖

class State {
public:
    TreeNode* node;
    int depth;

    State(TreeNode* node, int depth) : node(node), depth(depth) {}
};

void levelOrderTraverse(TreeNode* root) {
    if (root == nullptr) {
        return;
    }
    queue<State> q;
    // the path weight sum of the root node is 1
    q.push(State(root, 1));

    while (!q.empty()) {
        State cur = q.front();
        q.pop();
        // visit the cur node, while knowing its path weight sum
        cout << "depth = " << cur.depth << ", val = " << cur.node->val << endl;

        // add the left and right children of cur to the queue
        if (cur.node->left != nullptr) {
            q.push(State(cur.node->left, cur.depth + 1));
        }
        if (cur.node->right != nullptr) {
            q.push(State(cur.node->right, cur.depth + 1));
        }
    }
}

python 🤖

class State:
    def __init__(self, node, depth):
        self.node = node
        self.depth = depth

def levelOrderTraverse(root):
    if root is None:
        return
    q = deque()
    # the path weight sum of the root node is 1
    q.append(State(root, 1))

    while q:
        cur = q.popleft()
        # visit the cur node, and know its path weight sum
        print(f"depth = {cur.depth}, val = {cur.node.val}")

        # add the left and right child nodes of cur to the queue
        if cur.node.left is not None:
            q.append(State(cur.node.left, cur.depth + 1))
        if cur.node.right is not None:
            q.append(State(cur.node.right, cur.depth + 1))

go 🤖

type State struct {
    node  *TreeNode
    depth int
}

func levelOrderTraverse(root *TreeNode) {
    if root == nil {
        return
    }
    q := []State{{root, 1}}

    for len(q) > 0 {
        cur := q[0]
        q = q[1:]
        // visit the cur node, also know its path weight sum
        fmt.Printf("depth = %d, val = %d\n", cur.depth, cur.node.Val)

        // add cur's left and right children to the queue
        if cur.node.Left != nil {
            q = append(q, State{cur.node.Left, cur.depth + 1})
        }
        if cur.node.Right != nil {
            q = append(q, State{cur.node.Right, cur.depth + 1})
        }
    }
}

javascript 🤖

function State(node, depth) {
    this.node = node;
    this.depth = depth;
}

var levelOrderTraverse = function(root) {
    if (root === null) {
        return;
    }
    // @visualize bfs
    var q = [];
    // the path weight sum of the root node is 1
    q.push(new State(root, 1));

    while (q.length !== 0) {
        var cur = q.shift();
        // visit the cur node, while knowing its path weight sum
        console.log("depth = " + cur.depth + ", val = " + cur.node.val);

        // add the left and right children of cur to the queue
        if (cur.node.left !== null) {
            q.push(new State(cur.node.left, cur.depth + 1));
        }
        if (cur.node.right !== null) {
            q.push(new State(cur.node.right, cur.depth + 1));
        }
    }
};

You can open this visual panel and click on the line of code with console.log. This will allow you to see the tree nodes being traversed layer by layer from left to right, along with the level of each node:

With this approach, each node has its own depth variable, which is the most flexible and can meet all BFS algorithm needs. However, defining an additional State class can be cumbersome, so it's usually sufficient to use the second approach unless necessary.

You'll soon learn that scenarios with weighted edges belong to graph algorithms and will be used in the upcoming BFS Algorithm Exercises and Dijkstra's Algorithm.

Other Traversal Methods?

There are only the two traversal methods mentioned above for binary trees. There may be different ways to write them, but fundamentally, they cannot deviate from these two methods.

For instance, you might see code that uses a stack to iteratively traverse a binary tree. However, this is essentially still a recursive traversal, just manually maintaining a stack to simulate the recursive calls.

Similarly, you might see code that recursively traverses a binary tree layer by layer. But this is essentially level order traversal, just presenting the for loop in the level order traversal code in a recursive format.

In summary, don't be confused by appearances. The traversal methods for binary trees are just these two. Once you master these two methods with the following tutorials and exercises, all brute-force algorithms will be a piece of cake.

Why BFS is Often Used to Find the Shortest Path

By using a visual panel along with an example problem, you'll understand immediately.

Consider LeetCode Problem 111, "Minimum Depth of Binary Tree":

111. Minimum Depth of Binary Tree | LeetCode |

Given a binary tree, find its minimum depth.

The minimum depth is the number of nodes along the shortest path from the root node down to the nearest leaf node.

Note: A leaf is a node with no children.

Example 1:

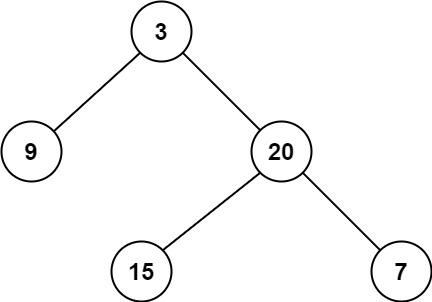
Input: root = [3,9,20,null,null,15,7]
Output: 2

Example 2:

Input: root = [2,null,3,null,4,null,5,null,6]
Output: 5

Constraints:

The number of nodes in the tree is in the range [0, 10⁵].
-1000 <= Node.val <= 1000

The minimum depth of a binary tree is the "distance from the root node to the nearest leaf node," so essentially, this problem is about finding the shortest distance.

Both DFS recursive traversal and BFS level-order traversal can solve this problem. Let's first look at the DFS recursive traversal solution:

java 🟢

class Solution {
    // record the minimum depth (the distance from the root to the nearest leaf node)
    private int minDepth = Integer.MAX_VALUE;
    // record the depth of the current node being traversed
    private int currentDepth = 0;

    public int minDepth(TreeNode root) {
        if (root == null) {
            return 0;
        }
        // start DFS traversal from the root node
        traverse(root);
        return minDepth;
    }

    private void traverse(TreeNode root) {
        if (root == null) {
            return;
        }

        // increase the current depth when entering a node in the preorder position
        currentDepth++;

        // if the current node is a leaf, update the minimum depth
        if (root.left == null && root.right == null) {
            minDepth = Math.min(minDepth, currentDepth);
        }

        traverse(root.left);
        traverse(root.right);

        // decrease the current depth when leaving a node in the postorder position
        currentDepth--;
    }
}

cpp 🤖

class Solution {
private:
    // record the minimum depth (the distance from the root to the nearest leaf node)
    int minDepthValue = INT_MAX;
    // record the depth of the current node being traversed
    int currentDepth = 0;

public:
    int minDepth(TreeNode* root) {
        if (root == nullptr) {
            return 0;
        }

        // start DFS traversal from the root node
        traverse(root);
        return minDepthValue;
    }

    void traverse(TreeNode* root) {
        if (root == nullptr) {
            return;
        }

        // increase the current depth when entering a node in the preorder position
        currentDepth++;

        // if the current node is a leaf, update the minimum depth
        if (root->left == nullptr && root->right == nullptr) {
            minDepthValue = min(minDepthValue, currentDepth);
        }

        traverse(root->left);
        traverse(root->right);

        // decrease the current depth when leaving a node in the postorder position
        currentDepth--;
    }
};

python 🤖

class Solution:
    def __init__(self):
        # record the minimum depth (the distance from the root to the nearest leaf node)
        self.minDepthValue = float('inf')
        # record the depth of the current node being traversed
        self.currentDepth = 0

    def minDepth(self, root: TreeNode) -> int:
        if root is None:
            return 0

        # start DFS traversal from the root node
        self.traverse(root)
        return self.minDepthValue

    def traverse(self, root: TreeNode) -> None:
        if root is None:
            return

        # increase the current depth when entering a node in the preorder position
        self.currentDepth += 1

        # if the current node is a leaf, update the minimum depth
        if root.left is None and root.right is None:
            self.minDepthValue = min(self.minDepthValue, self.currentDepth)

        self.traverse(root.left)
        self.traverse(root.right)

        # decrease the current depth when leaving a node in the postorder position
        self.currentDepth -= 1

go 🤖

func minDepth(root *TreeNode) int {
    if root == nil {
        return 0
    }

    // record the minimum depth (the distance from the root to the nearest leaf node)
    minDepthValue := math.MaxInt32
    // record the depth of the current node being traversed
    currentDepth := 0

    var traverse func(*TreeNode)
    traverse = func(root *TreeNode) {
        if root == nil {
            return
        }

        // increase the current depth when entering a node in the preorder position
        currentDepth++

        // if the current node is a leaf, update the minimum depth
        if root.Left == nil && root.Right == nil {
            minDepthValue = min(minDepthValue, currentDepth)
        }

        traverse(root.Left)
        traverse(root.Right)

        // decrease the current depth when leaving a node in the postorder position
        currentDepth--
    }

    // start DFS traversal from the root node
    traverse(root)
    return minDepthValue
}

javascript 🤖

var minDepth = function(root) {
    if (root === null) {
        return 0;
    }
    
    // record the minimum depth (the distance from the root to the nearest leaf node)
    let minDepthValue = Infinity;

    // record the depth of the current node being traversed
    let currentDepth = 0;

    const traverse = function(root) {
        if (root === null) {
            return;
        }

        // increase the current depth when entering a node in the preorder position
        currentDepth++;

        // if the current node is a leaf, update the minimum depth
        if (root.left === null && root.right === null) {
            minDepthValue = Math.min(minDepthValue, currentDepth);
        }

        traverse(root.left);
        traverse(root.right);

        // decrease the current depth when leaving a node in the postorder position
        currentDepth--;
    };

    // start DFS traversal from the root node
    traverse(root);
    return minDepthValue;
};

You can open the visualization panel below and click on the line if (root === null) to see the order in which the recursive function traverse visits the nodes of the binary tree. To put it simply, it traverses from left to right, branch by branch:

When the leaf node of a branch is reached, the minimum depth is updated. After traversing the entire tree, you can calculate the minimum depth of the whole tree.

Is it possible to terminate the algorithm early without traversing the entire tree? No, because you need to know the depth of each branch (the distance from the root node to the leaf node) to find the smallest one.

Now, let's look at the BFS level-order traversal solution. With BFS, which traverses the binary tree level by level from top to bottom, the minimum depth can be determined when the first leaf node is reached:

java 🟢

class Solution {
    public int minDepth(TreeNode root) {
        if (root == null) return 0;
        Queue<TreeNode> q = new LinkedList<>();
        q.offer(root);
        // the root itself is one layer, initialize depth to 1
        int depth = 1;

        while (!q.isEmpty()) {
            int sz = q.size();
            // traverse the nodes of the current layer
            for (int i = 0; i < sz; i++) {
                TreeNode cur = q.poll();
                // check if we have reached a leaf node
                if (cur.left == null && cur.right == null)
                    return depth;
                // add the nodes of the next layer to the queue
                if (cur.left != null)
                    q.offer(cur.left);
                if (cur.right != null)
                    q.offer(cur.right);
            }
            // increment the depth here
            depth++;
        }
        return depth;
    }
}

cpp 🤖

class Solution {
public:
    int minDepth(TreeNode* root) {
        if (root == nullptr) return 0;
        queue<TreeNode*> q;
        q.push(root);
        // the root itself is one layer, initialize depth to 1
        int depth = 1;

        while (!q.empty()) {
            int sz = q.size();
            // traverse the nodes of the current layer
            for (int i = 0; i < sz; i++) {
                TreeNode* cur = q.front();
                q.pop();
                // check if we have reached a leaf node
                if (cur->left == nullptr && cur->right == nullptr)
                    return depth;
                // add the nodes of the next layer to the queue
                if (cur->left != nullptr)
                    q.push(cur->left);
                if (cur->right != nullptr)
                    q.push(cur->right);
            }
            // increment the depth here
            depth++;
        }
        return depth;
    }
};

python 🤖

class Solution:
    def minDepth(self, root: TreeNode) -> int:
        if root is None:
            return 0
        q = deque([root])
        # the root itself is one layer, initialize depth to 1
        depth = 1

        while q:
            sz = len(q)
            # traverse the nodes of the current layer
            for _ in range(sz):
                cur = q.popleft()
                # check if we have reached a leaf node
                if cur.left is None and cur.right is None:
                    return depth
                # add the nodes of the next layer to the queue
                if cur.left is not None:
                    q.append(cur.left)
                if cur.right is not None:
                    q.append(cur.right)
            # increment the depth here
            depth += 1
        return depth

go 🤖

func minDepth(root *TreeNode) int {
    if root == nil {
        return 0
    }
    q := []*TreeNode{root}
    // the root itself is one layer, initialize depth to 1
    depth := 1

    for len(q) > 0 {
        sz := len(q)
        // traverse the nodes of the current layer
        for i := 0; i < sz; i++ {
            cur := q[0]
            q = q[1:]
            // check if we have reached a leaf node
            if cur.Left == nil && cur.Right == nil {
                return depth
            }
            // add the nodes of the next layer to the queue
            if cur.Left != nil {
                q = append(q, cur.Left)
            }
            if cur.Right != nil {
                q = append(q, cur.Right)
            }
        }
        // increment the depth here
        depth++
    }
    return depth
}

javascript 🤖

var minDepth = function(root) {
    if (root === null) return 0;
    let q = [root];
    // the root itself is one layer, initialize depth to 1
    let depth = 1;

    while (q.length > 0) {
        let sz = q.length;
        // traverse the nodes of the current layer
        for (let i = 0; i < sz; i++) {
            let cur = q.shift();
            // check if we have reached a leaf node
            if (cur.left === null && cur.right === null)
                return depth;
            // add the nodes of the next layer to the queue
            if (cur.left !== null)
                q.push(cur.left);
            if (cur.right !== null)
                q.push(cur.right);
        }
        // increment the depth here
        depth++;
    }
    return depth;
};

You can open the visualization panel below and click on the line if (cur.left === null && cur.right === null) to see how BFS traverses the binary tree nodes level by level:

When it reaches the second line, it encounters the first leaf node. This leaf node is the one closest to the root, so the algorithm terminates at this point.

Click on the code segment let result = to observe the colors of the nodes in the binary tree. You will see that the BFS algorithm finds the minimum depth without traversing the entire tree.

In summary, you should understand why BFS is often used to find the shortest path:

Due to the level-by-level traversal logic of BFS, the path taken when the target node is first encountered is the shortest path. The algorithm may not need to traverse all nodes to finish early.

DFS can also be used to find the shortest path, but it must traverse all nodes to obtain the shortest path.

From a time complexity perspective, both algorithms will traverse all nodes in the worst case, with a time complexity of $O(N)$ . However, in general scenarios, BFS is more efficient. Therefore, for shortest path problems, BFS is the preferred algorithm.

Why DFS is Commonly Used to Find All Paths

When it comes to finding all paths, you'll notice that the Depth-First Search (DFS) algorithm is used more frequently, while the Breadth-First Search (BFS) algorithm is not as commonly applied.

In theory, both traversal algorithms can be used. However, the code for BFS to find all paths is more complex, whereas the code for DFS is more straightforward.

Consider a binary tree as an example. To use BFS to find all paths (from the root node to each leaf node), the queue cannot only contain nodes. Instead, you would need a third approach, creating a State class to store both the current node and the path taken to reach it. This method ensures each node's path is correctly maintained, allowing for the calculation of all paths.

On the other hand, using DFS is simpler. DFS naturally traverses the tree branch by branch from left to right, with each branch representing a path. Hence, DFS is inherently suitable for finding all paths.

Finally, let's combine the code with a visualization panel for explanation. First, examine the visualization panel for the DFS algorithm. You can repeatedly click on the if (root === null) part of the code to observe how DFS traverses all nodes and collects all paths from the root to the leaf nodes:

Next, look at the visualization panel for the BFS algorithm. By repeatedly clicking on the if (node.left === null && node.right === null) part of the code, you can observe how BFS traverses all nodes and collects all paths from the root to the leaf nodes. Hovering over the generated BFS tree nodes below will show the path stored in each State:

From the JavaScript code in the visualization panel, it is apparent that BFS code is more complex.

In summary, the DFS algorithm is more commonly used for finding all paths, while BFS is typically used for finding the shortest path.

Binary Tree Recursive/Level Traversal

111. 二叉树的最小深度 https://leetcode.cn/problems/minimum-depth-of-binary-tree

111. Minimum Depth of Binary Tree https://leetcode.com/problems/minimum-depth-of-binary-tree

Recursive Traversal (DFS)

Level Order Traversal (BFS)

Method One

Approach Two

Approach Three

Other Traversal Methods?

Why BFS is Often Used to Find the Shortest Path

Why DFS is Commonly Used to Find All Paths