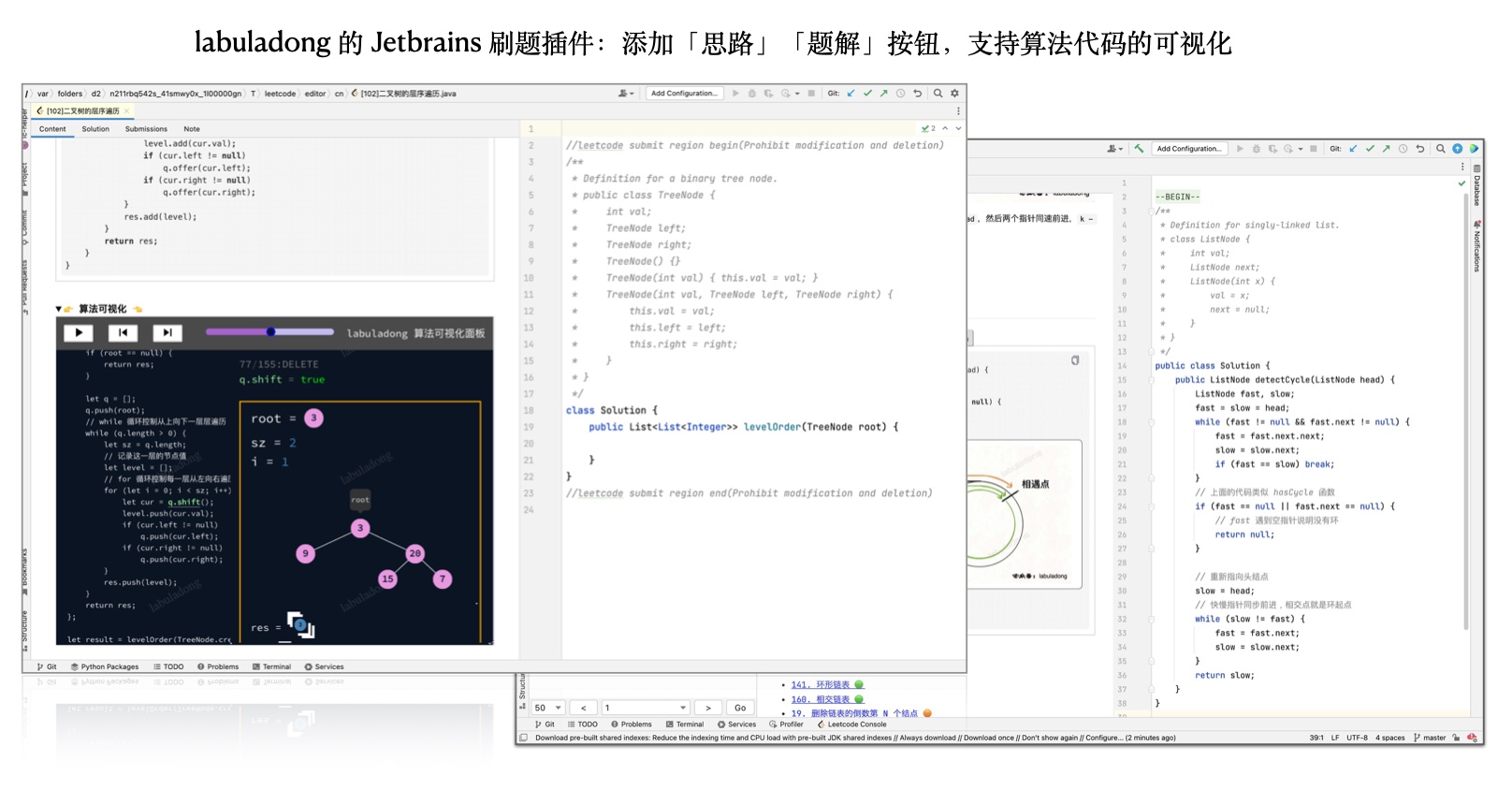
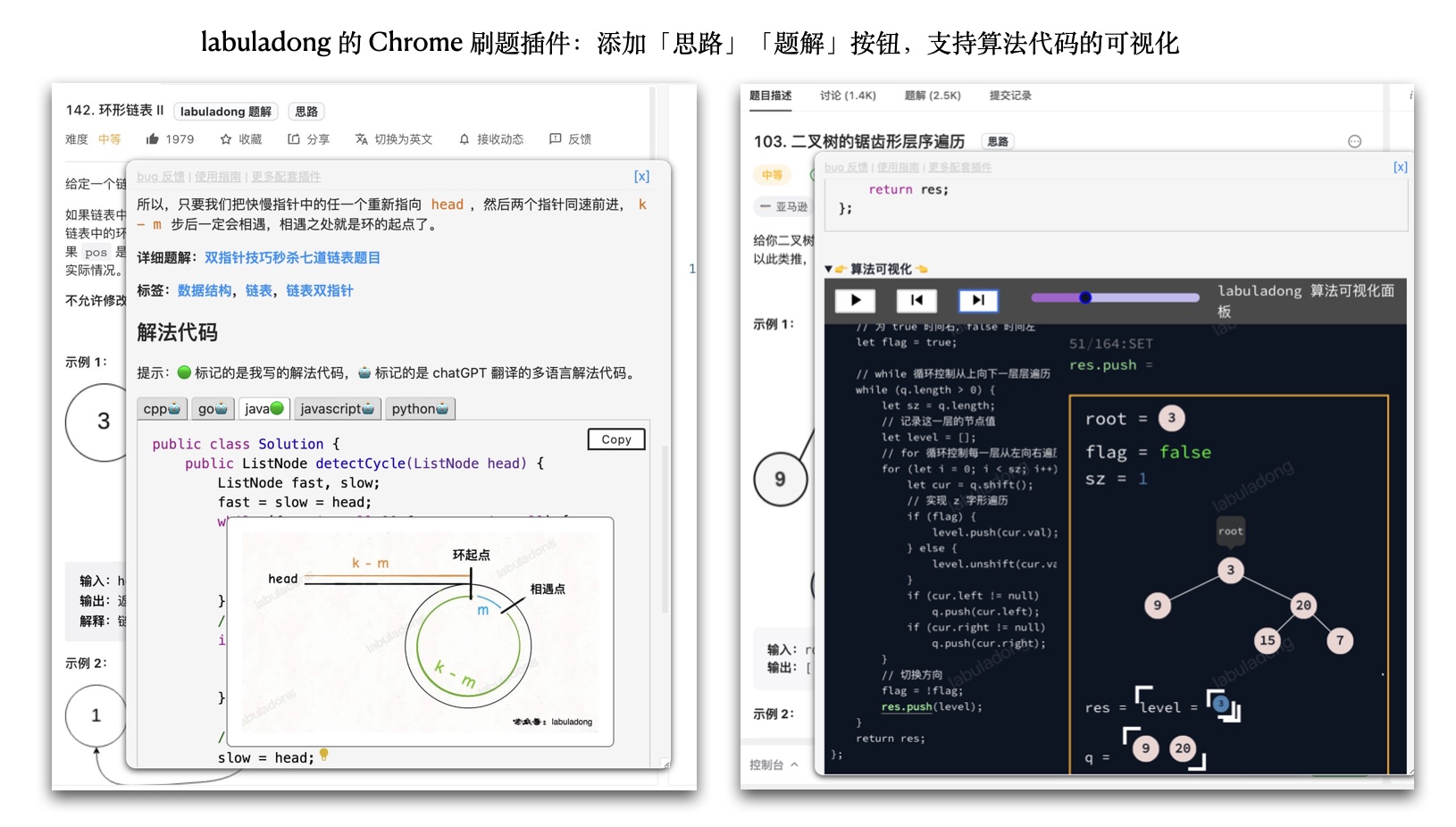
功能总览
算法可视化
可交互的算法可视化面板,所有题目代码下方都有对应的可视化面板。
🚀 递归可视化示例 🚀
图片注释
对于比较复杂的算法,代码中会包含小灯泡图标,鼠标移动到图标上会弹出对应的图片,辅助理解算法。
网站和所有配套插件均已适配此功能
java 🟢
class Solution {
public ListNode detectCycle(ListNode head) {
ListNode fast, slow;
fast = slow = head;
while (fast != null && fast.next != null) {
fast = fast.next.next;
slow = slow.next;
if (fast == slow) break;/**<extend down -200><div class="img-content"><img src="/algo/images/双指针/3.jpeg" class="myimage"/></div> */
}
// 上面的代码类似 hasCycle 函数
if (fast == null || fast.next == null) {
// fast 遇到空指针说明没有环
return null;
}
// 重新指向头结点
slow = head;/**<extend up -100><div class="img-content"><img src="/algo/images/双指针/2.jpeg" class="myimage"/></div> */
// 快慢指针同步前进,相交点就是环起点
while (slow != fast) {
fast = fast.next;
slow = slow.next;
}
return slow;
}
}cpp 🤖
// cpp 代码由 chatGPT🤖 根据我的 java 代码翻译,旨在帮助不同背景的读者理解算法逻辑。
class Solution {
public:
ListNode *detectCycle(ListNode *head) {
ListNode *fast, *slow;
fast = slow = head;
while (fast != nullptr && fast->next != nullptr) {
fast = fast->next->next;
slow = slow->next;
if (fast == slow) break;/**<extend down -200><div class="img-content"><img src="/algo/images/双指针/3.jpeg" class="myimage"/></div> */
}
// 上面的代码类似 hasCycle 函数
if (fast == nullptr || fast->next == nullptr) {
// fast 遇到空指针说明没有环
return nullptr;
}
// 重新指向头结点
slow = head;/**<extend up -100><div class="img-content"><img src="/algo/images/双指针/2.jpeg" class="myimage"/></div> */
// 快慢指针同步前进,相交点就是环起点
while (slow != fast) {
fast = fast->next;
slow = slow->next;
}
return slow;
}
};python 🤖
# python 代码由 chatGPT🤖 根据我的 java 代码翻译,旨在帮助不同背景的读者理解算法逻辑。
class Solution:
def detectCycle(self, head: ListNode):
"""
:type head: ListNode
:rtype: ListNode
"""
fast, slow = head, head
while fast and fast.next:
fast = fast.next.next
slow = slow.next
if fast == slow:
break # <extend down -200><div class="img-content"><img src="/algo/images/双指针/3.jpeg" class="myimage"/></div> #
# 上面的代码类似 hasCycle 函数
if not fast or not fast.next:
# fast 遇到空指针说明没有环
return None
# 重新指向头结点
slow = head # <extend up -100><div class="img-content"><img src="/algo/images/双指针/2.jpeg" class="myimage"/></div> #
# 快慢指针同步前进,相交点就是环起点
while slow != fast:
fast = fast.next
slow = slow.next
return slowgo 🤖
// go 代码由 chatGPT🤖 根据我的 java 代码翻译,旨在帮助不同背景的读者理解算法逻辑。
func detectCycle(head *ListNode) *ListNode {
fast, slow := head, head
for fast != nil && fast.Next != nil {
fast = fast.Next.Next
slow = slow.Next
if fast == slow {
break/**<extend down -200><div class="img-content"><img src="/algo/images/双指针/3.jpeg" class="myimage"/></div> */
}
}
if fast == nil || fast.Next == nil {
return nil
}
slow = head/**<extend up -100><div class="img-content"><img src="/algo/images/双指针/2.jpeg" class="myimage"/></div> */
for slow != fast {
fast = fast.Next
slow = slow.Next
}
return slow
}javascript 🤖
// javascript 代码由 chatGPT🤖 根据我的 java 代码翻译,旨在帮助不同背景的读者理解算法逻辑。
/**
* @param {ListNode} head
* @return {ListNode}
*/
var detectCycle = function(head) {
let fast, slow;
fast = slow = head;
while (fast !== null && fast.next !== null) {
fast = fast.next.next;
slow = slow.next;
if (fast == slow) break;/**<extend down -200><div class="img-content"><img src="/algo/images/双指针/3.jpeg" class="myimage"/></div> */
}
// 上面的代码类似 hasCycle 函数
if (fast === null || fast.next === null) {
// fast 遇到空指针说明没有环
return null;
}
// 重新指向头结点
slow = head;/**<extend up -100><div class="img-content"><img src="/algo/images/双指针/2.jpeg" class="myimage"/></div> */
// 快慢指针同步前进,相交点就是环起点
while (slow !== fast) {
fast = fast.next;
slow = slow.next;
}
return slow;
};vscode 刷题插件
辅助功能和 Chrome 插件类似,方便不喜欢在网页上刷题的同学。
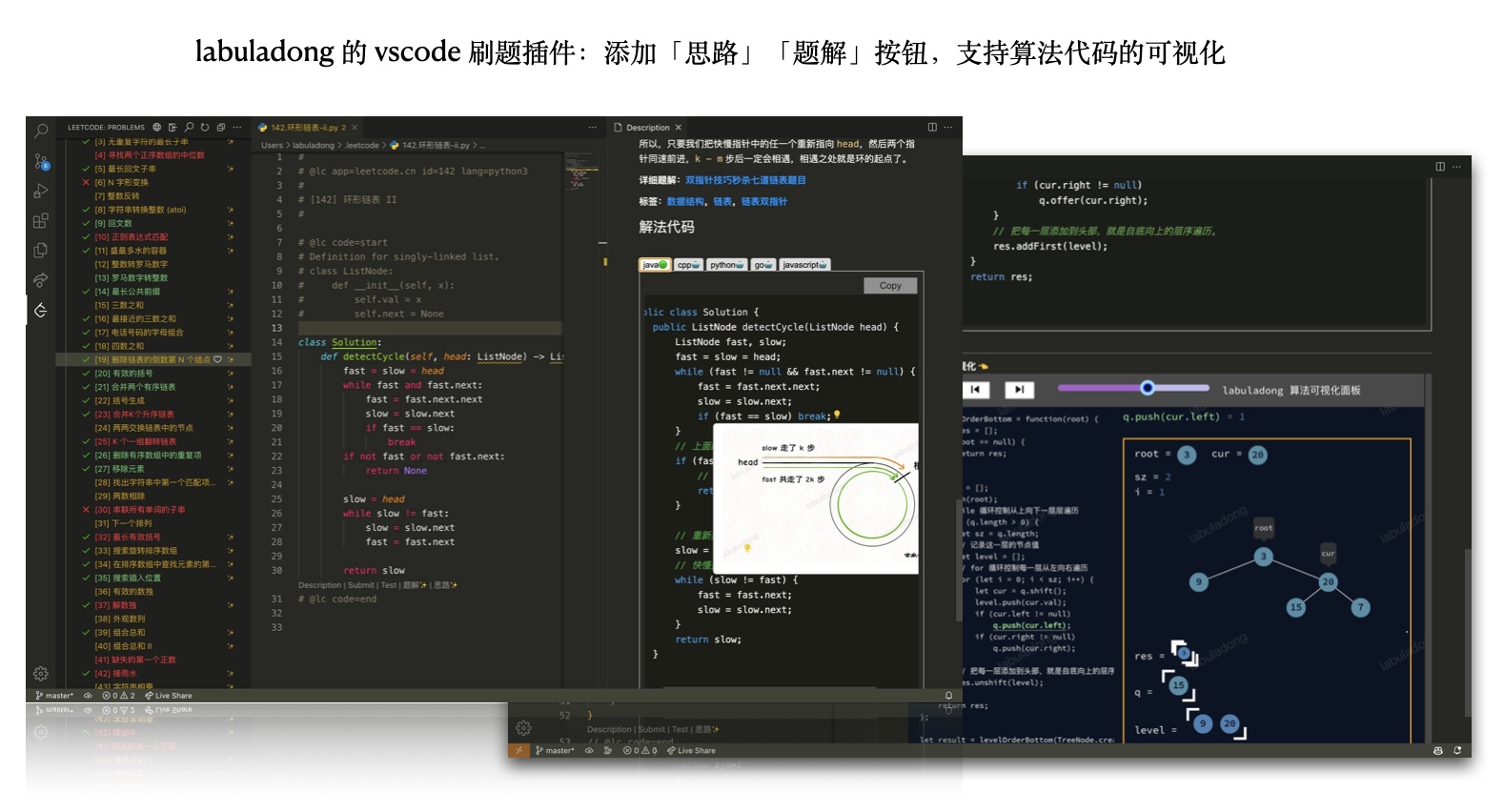
Jetbrains 刷题插件
辅助功能和 Chrome 插件类似,方便不喜欢在网页上刷题的同学。